AI Engine Development See Vitis™ Development Environment on xilinx.com See Vitis™ AI Development Environment on xilinx.com

Using Floating-Point in the AI Engine

Version: Vitis 2022.1

Introduction

The purpose of this set of examples is to understand floating-point vector computations within the AI Engine.

Before You Begin

Before starting to explore these examples, refer to the following documents:

• Versal® ACAP AI Engine architecture documentation

  • AI Engine Architecture

  • Versal ACAP AI Engines for Dummies

  • Architecture Details Summary

• Tools and documentation lounge

  • AI Engine Tools lounge

  • UG1076: Versal ACAP AI Engine Programming Environment User Guide

• Also, download and install:

  • Vitis 2022.1 Download Vitis

  • Licenses for AI Engine tools.

  • Base Platform VCK190 Vitis Platform

Before starting this tutorial, set up your PLATFORM_REPO_PATHS environment variable based upon where you downloaded the platform.

AI Engine Architecture Details

Versal adaptive compute acceleration platforms (ACAPs) combine Scalar Engines, Adaptable Engines, and Intelligent Engines with leading-edge memory and interfacing technologies to deliver powerful heterogeneous acceleration for any application. Intelligent Engines are SIMD VLIW AI Engines for adaptive inference and advanced signal processing compute, and DSP Engines for fixed point, floating point, and complex MAC operations.

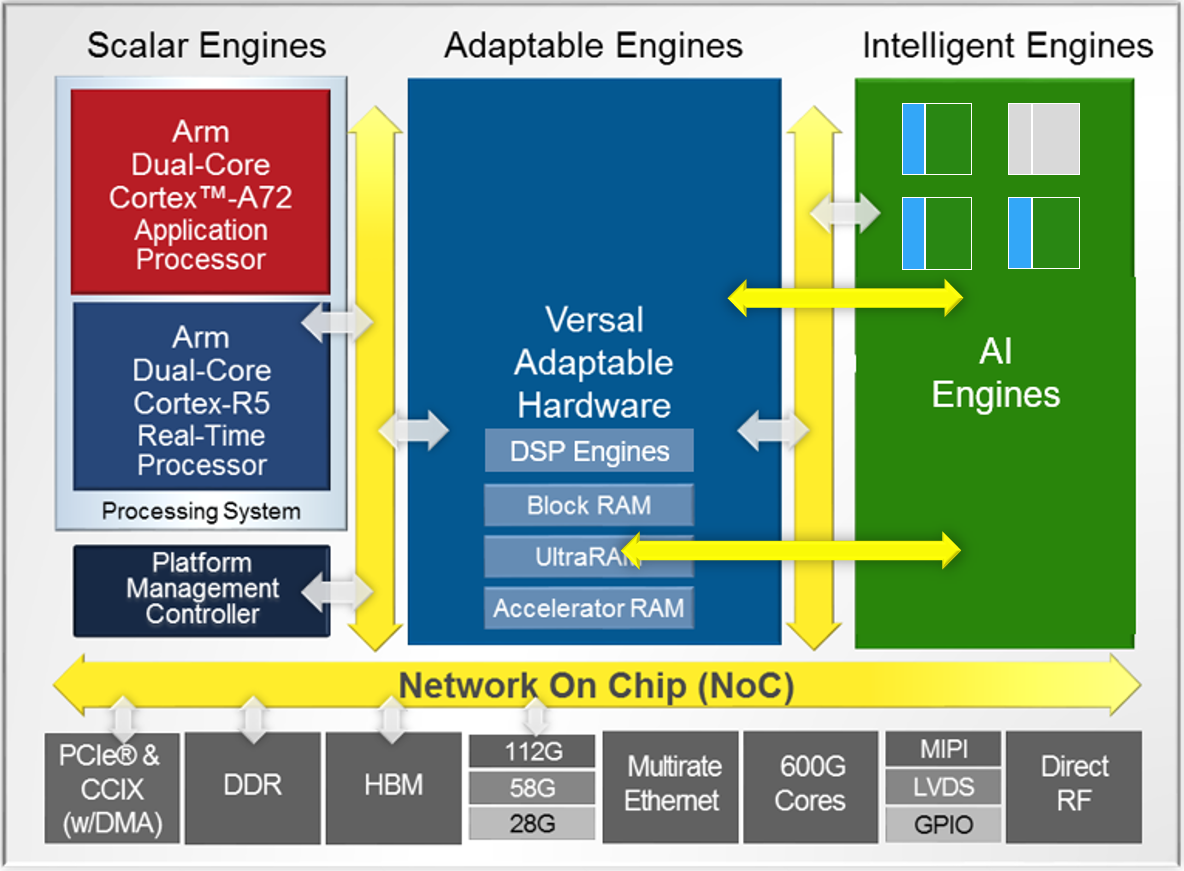
The Intelligent Engine comes as an array of AI Engines connected together using AXI-Stream interconnect blocks:

AI Engine array

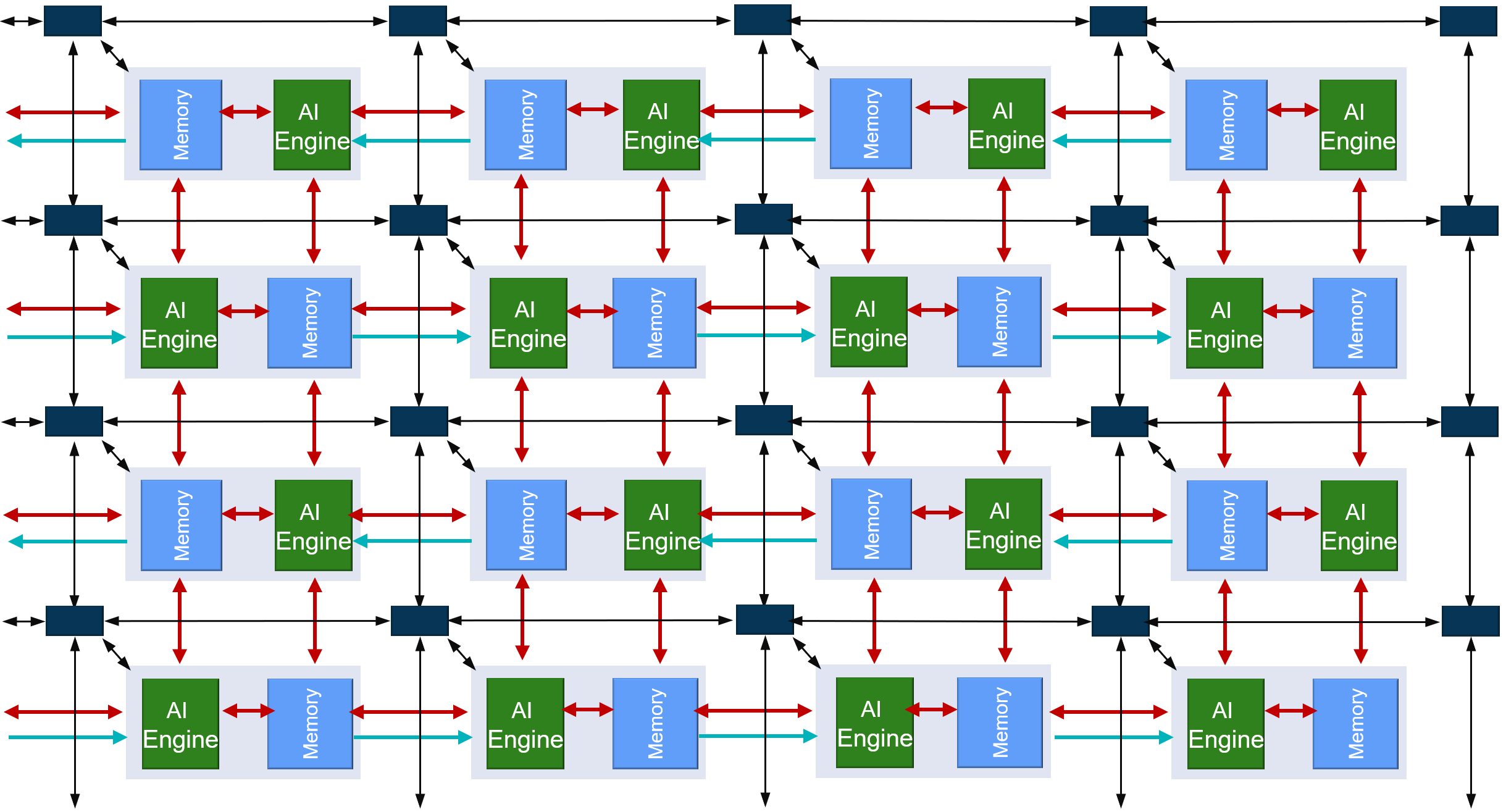
As seen in the image above, each AI Engine is connected to four memory modules on the four cardinal directions. The AI Engine and memory modules are both connected to the AXI-Stream interconnect.

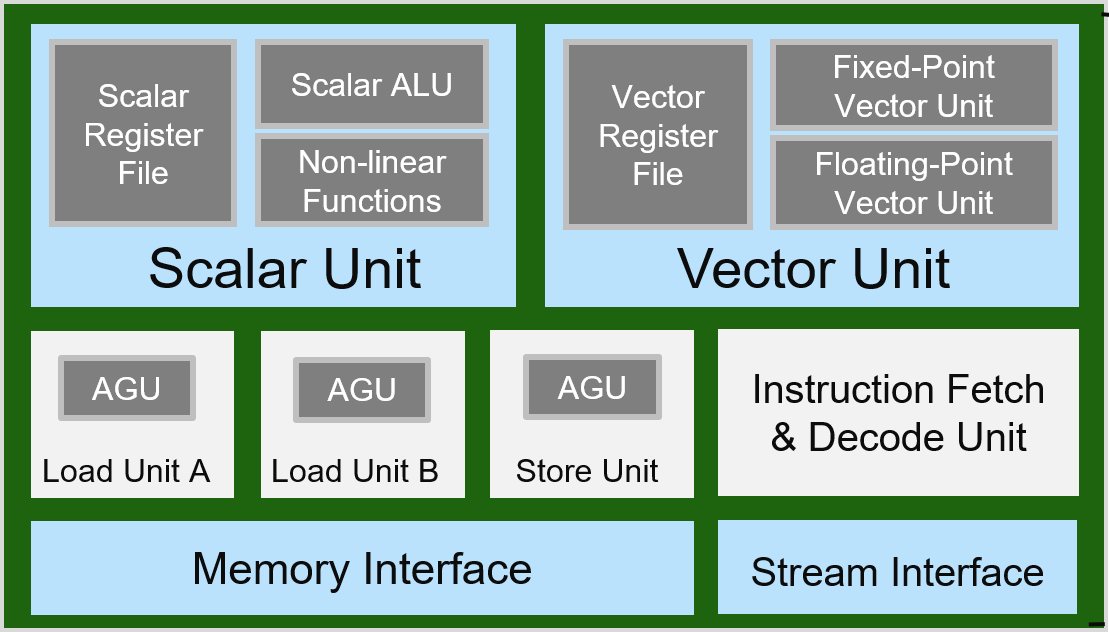
The AI Engine is a VLIW (7-way) processor that contains:

• Instruction Fetch and Decode Unit

• A Scalar Unit

• A Vector Unit (SIMD)

• Three Address Generator Units

• Memory and Stream Interface

AI Engine Module

Have a look at the fixed-point unit pipeline, as well as floating-point unit pipeline within the vector unit.

Fixed-Point Pipeline

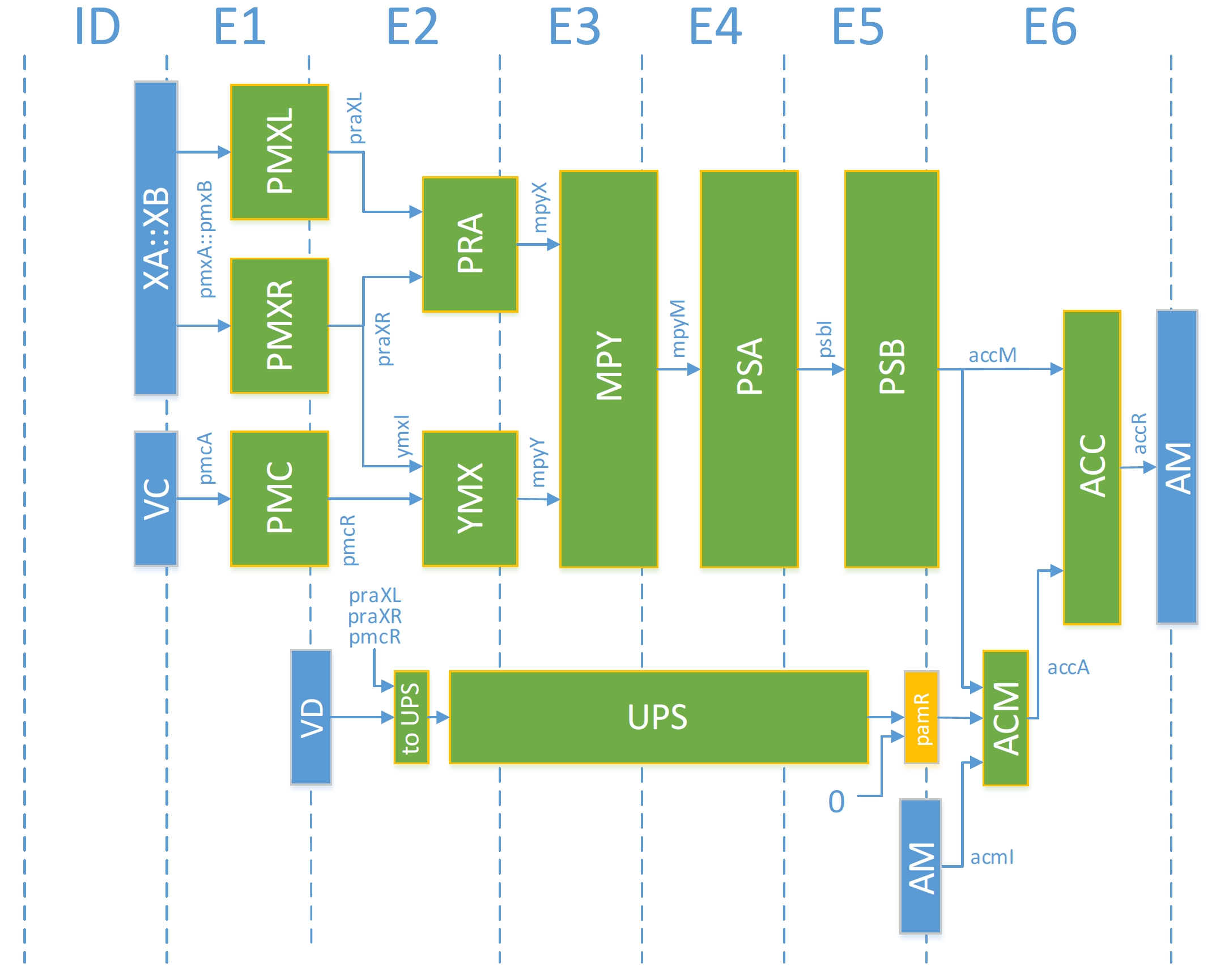
In this pipeline one can see the data selection and shuffling units; PMXL, PMXR, and PMC. The pre-add (PRA) is just before the multiply block and then two lane reduction blocks (PSA, PSB) allows to perform up to 128 multiplies and get an output on 16 lanes down to two lanes. The accumulator block is fed either by its own output (AM) or by the upshift output. The feedback on the ACC block is only one clock cycle.

Floating-point Pipeline

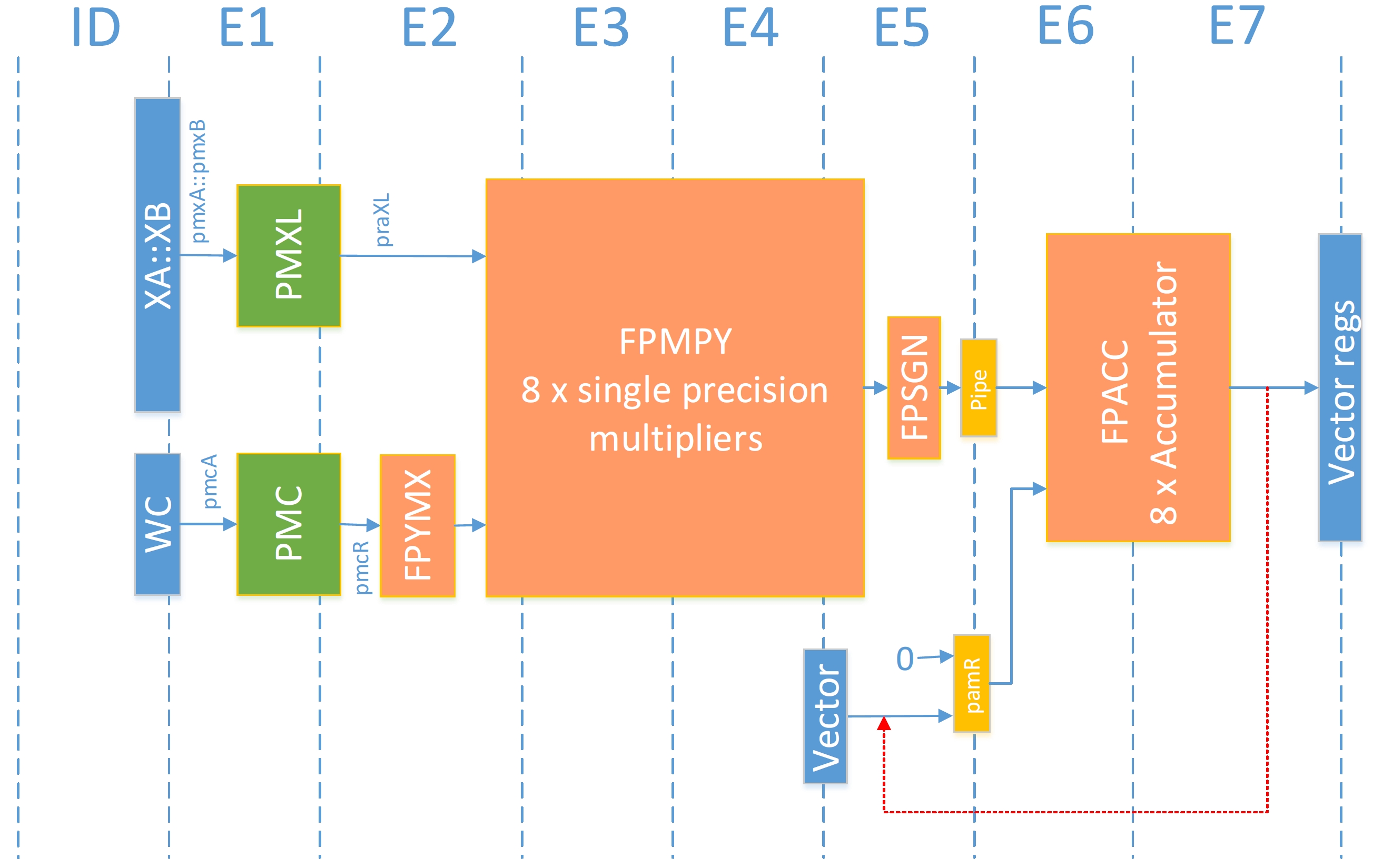
In this pipeline one can see that the selection and shuffling units (PMXL, PMC) are the same as in the fixed-point unit. Unlike the fixed-point pipeline there is no lane reduction unit, so the lanes that you have at the input will also be there at the output. Another difference is that the post-accumulator is on two clock cycles. If the goal is to reuse the same accumulator over and over, only one fpmac per two clock cycles can be issued.

Floating-point intrinsics

There is a limited set of intrinsics with which a multitude of operations can be performed. All of them return either a v8float or v4cfloat, 256-bit vectors.

The basic addition, subtraction, and negation functions are as follows:

• fpadd

• fpadd_abs

• fpsub

• fpsub_abs

• fpneg

• fpneg_abs

• fpabs

The simple multiplier function is available with the following options:

• fpmul

• fpabs_mul

• fpneg_mul

• fpneg_abs_mul

The multiplication accumulation/subtraction function has the following options:

• fpmac

• fpmac_abs

• fpmsc

• fpmsc_abs

On top of these various intrinsics you have a fully configurable version multiplier and multiply-accumulate:

• fpmul_conf

• fpmac_conf

Start, offset

In all the subsequent intrinsics, the input vector(s) go through a data shuffling function that is controlled by two parameters:

• Start

• Offset

Let us take the fpmul function:

v8float fpmul(v32float xbuf, int xstart, unsigned int xoffs, v8float zbuf, int zstart, unsigned int zoffs)

• xbuf, xstart, xoffs: first buffer and shuffling parameters

• zbuf, zstart, zoffs: second buffer and shuffling parameters

• Start: starting offset for all lanes of the buffer

• Offset: additional, lane-dependent offset for the buffer. Definition takes 4 bits per lane.

For example:

v8float ret = fpmul(xbuf,2,0x210FEDCB,zbuf,7,0x76543210)

for (i = 0 ; i < 8 ; i++)
  ret[i] =  xbuf[xstart + xoffs[i]] * zbuf[zstart + zoffs[i]]

All values in hexadecimal:

ret Index (Lane)		xbuf Start	xbuf Offset	Final xbuf Index		zbuf Start	zbuf Offset	Final zbuf Index
0		2	B	D		7	0	7
1		2	C	E		7	1	8
2		2	D	F		7	2	9
3		2	E	10		7	3	A
4		2	F	11		7	4	B
5		2	0	2		7	5	C
6		2	1	3		7	6	D
7		2	2	4		7	7	E

fpneg, fpabs, fpadd, fpsub

fpneg

Output is the opposite of its input. Input can be either float or cfloat forming a 512-bit or a 1024-bit buffer (v32float, v16float, v16cfloat, v8cfloat). The output is a 256-bit buffer as all the floating-point operators (v8float, v4cfloat).

v8float fpneg (v32float xbuf, int xstart, unsigned int xoffs)

for (i = 0 ; i < 8 ; i++)
  ret[i] = - xbuf[xstart + xoffs[i]]

fpabs

Output is the absolute value of the input. It takes only real floating-point input vectors.

fpneg_abs

Output is the negation of the absolute value of the input. It takes only real floating-point input vectors.

fpadd, fpsub

Output is the sum (the subtraction) of the input buffers.

v8float fpadd (v8float acc, v32float xbuf, int xstart, unsigned int xoffs)

Parameter	Comment
acc	First addition input buffer. It has the same type as the output
xbuf	Second addition input buffer.
xstart	Starting offset for all lanes of X.
xoffs	4 bits per lane: Additional lane-dependent offset for X.

The executed operation is:

for (i = 0 ; i < 8 ; i++)
  ret[i] = acc[i] + xbuf[xstart + xoffs[i]]

Allowed datatypes:

• acc: v8float, v4cfloat

• xbuf: v32float, v16float, v16cfloat, v8cfloat

fpadd_abs, fpsub_abs

Adds or subtracts the absolute value of the second buffer to the first one.

for (i = 0 ; i < 8 ; i++)
  ret[i] = acc[i] +/- abs(xbuf[xstart + xoffs[i]])

fpmul

The simple floating-point multiplier comes in many different flavors mixing or not float and cfloat vector data types. When two cfloat are involved, the intrinsic results in two microcode instructions that must be scheduled. The first buffer can be either 512 or 1024-bit long (v32float, v16float, v16cfloat, v8cfloat), the second buffer is always 256-bit long (v8float, v4cfloat). Any combination is allowed.

v8float fpmul(v32float xbuf, int xstart, unsigned int xoffs, v8float zbuf, int zstart, unsigned int zoffs)

Returns the multiplication result.

Parameter	Comment
xbuf	First multiplication input buffer.
xstart	Starting offset for all lanes of X.
xoffs	4 bits per lane, additional lane-dependent offset for X.
zbuf	Second multiplication input buffer.
zstart	Starting offset for all lanes of Z. This must be a compile time constant.
zoffs	4 bits per lane, additional lane-dependent offset for Z.

for (i = 0 ; i < 8 ; i++)
  ret[i] =  xbuf[xstart + xoffs[i]] * zbuf[zstart + zoffs[i]]

fpabs_mul

Only for real arguments. Signature is identical to fpmul:

v8float fpabs_mul(v32float xbuf, int xstart, unsigned int xoffs, v8float zbuf, int zstart, unsigned int zoffs)

It returns the absolute value of the product:

for (i = 0 ; i < 8 ; i++)
  ret[i] =  abs(xbuf[xstart + xoffs[i]] * zbuf[zstart + zoffs[i]])

fpneg_mul

Signature is identical to fpmul:

v8float fpneg_mul(v32float xbuf, int xstart, unsigned int xoffs, v8float zbuf, int zstart, unsigned int zoffs)

It returns the opposite value of the product:

for (i = 0 ; i < 8 ; i++)
  ret[i] =  - xbuf[xstart + xoffs[i]] * zbuf[zstart + zoffs[i]]

fpneg_abs_mul

Only for real arguments. Signature is identical to fpmul:

v8float fpneg_mul(v32float xbuf, int xstart, unsigned int xoffs, v8float zbuf, int zstart, unsigned int zoffs)

It returns the opposite value of the product:

for (i = 0 ; i < 8 ; i++)
  ret[i] =  - xbuf[xstart + xoffs[i]] * zbuf[zstart + zoffs[i]]

fpmac, fpmsc, fpmac_abs, fpmsc_abs

For all these functions there is one more argument compared to the fpmul function. This is the previous value of the accumulator.

v8float fpmac(v8float acc, v32float xbuf, int xstart, unsigned int xoffs, v8float zbuf, int zstart, unsigned int zoffs)

• fpmac : multiply operands and add to the accumulator

• fpmsc : multiply operands and subtract from the accumulator

• fpmac_abs : multiply operands and add the absolute value to the accumulator

• fpmsc_abs : multiply operands and subtract the absolute value from the accumulator

The two “abs” variants are available only for real arguments.

fpmul_conf, fpmac_conf

These functions are fully configurable fpmul and fpmac functions. The output can be considered to always have eight values because each part of the complex float is treated differently A v4cfloat will have the loop interating over real0 - complex0 - real1 - complex1 … This capability is introduced to allow flexibility and implement operations on conjugates.

v8float fpmac_conf(v8float acc, v32float xbuf, int xstart, unsigned int xoffs, v8float zbuf, int zstart, unsigned int zoffs, bool ones, bool abs, unsigned int addmode, unsigned int addmask, unsigned int cmpmode, unsigned int & cmp)

Returns the multiplication result.

Parameter	Comment
acc	Current accumulator value. This parameter does not exist for fpmul_conf.
xbuf	First multiplication input buffer.
xstart	Starting offset for all lanes of X.
xoffs	4 bits per lane: Additional lane-dependent offset for X.
zbuf	Optional Second multiplication input buffer. If zbuf is not specified, xbuf is taken as the second buffer
zstart	Starting offset for all lanes of Z. This must be a compile time constant.
zoffs	4 bits per lane: Additional lane-dependent offset for Z.
ones	If true all lanes from Z are replaced with 1.0.
abs	If true the absolute value is taken before accumulation.
addmode	Select one of fpadd_add (all add), fpadd_sub (all sub), fpadd_mixadd or fpadd_mixsub (add-sub or sub-add pairs). This must be a compile time constant.
addmask	8 x 1 LSB bits: Corresponding lane is negated if bit is set (depending on addmode).
cmpmode	Use "fpcmp_lt" to select the minimum between accumulator and result of multiplication per lane, "fpcmp_ge" for the maximum and "fpcmp_nrm" for the usual sum.
cmp	Optional 8 x 1 LSB bits: When using fpcmp_ge or fpcmp_lt in "cmpmode", it sets a bit if accumulator was chosen (per lane).

Floating-Point Examples

The purpose of this set of examples is to show how to use floating-point computations within the AI Engines in different schemes:

• FIR filter

• Matrix Multiply

FIR Filter

As there is no post-add lane reduction hardware in the floating-point pipeline of the AI Engine, all outputs will always be on eight lanes (float) or four lanes (cfloat). This means that we can compute eight (four) lanes in parallel, each time with a single coefficient, using fpmul and then fpmac for all the coefficients, one by one.

The floating-point accumulator has a latency of two clock cycles, so two fpmac instructions using the same accumulator cannot be used back to back, but only every other cycle. Code can be optimized by using two accumulators, used in turn, that get added at the end to get the final result.

• Navigate to the FIRFilter directory.

• Type make all in the console and wait for completion of the three following stages:

  1. aie

  2. aiesim

  3. aieviz

The last stage is opening vitis_analyzer that will allow you to visualize the graph of the design and the simulation process timeline.

In this design you learned:

• How to use real floating-point data and coefficients in FIR filters.

• How to handle complex floating-point data and complex floating-points coefficients in FIR filters.

• How to organize the compute sequence.

• How to use: fpmul, fpmac, and fpadd in the real and complex case.

Real Floating-Point Filter

In the example, the filter has 16 coefficients which do not fit within a 256-bit register. The register must be updated in the middle of the computation.

For data storage a small 512-bit register is used. It is decomposed in two 256-bit parts: W0, W1.

• First iteration

  • Part W0 is loaded with first 8 samples (0…7)

  • Part W1 with the next 8 samples (8…15)

  • Part W0 with the following ones (16…23)

• Second iteration

  • Part W0 : 8…15

  • Part W1 : 16…23

  • Part W0 : 24…31

Complex Floating-Point Filter

cfloat x cfloat multiplications take two cycles to perform due to the abscence of the post add. These two parts can be interleaved with the two cycle latency of the accumulator.

There are still 16 coefficients but now they are complex, hence double the size. The coefficients have to be updated four times for a complete iteration. The data transfer is also slightly more complex.

Matrix Multiply

In this example, a matrix multiply (AB) example is shown with the simple fpmul and fpmac intrinsics in the real and complex case. In the complex case there are also two other examples using the fpmul_conf and fpmac_conf intrinsics to compute AB and A*conj(B).

Intrinsics being lane by lane computation oriented, this feature will be used to compute a number of consecutive columns of the output matrix. The latency of two of the accumulator is absorbed by computing two rows of the output matrix.

All the parameter settings for the fpmul/mac_conf intrinsics are explained in the code itself.

• Navigate to the MatMult directory.

• Type make all in the console and wait for the completions of the 3 stages:

  1. aie

  2. aiesim

  3. aieviz

The last stage is opening vitis_analyzer that will allow you to visualize the graph of the design and the simulation process timeline.

In this design you learned:

• How to organize matrix multiply compute sequence when using real or complex floating-point numbers.

• How to handle complex floating-point data and complex floating-points coefficients in FIR filters.

• How to use fpmul_conf and fpmac_conf intrinsics.

License

Licensed under the Apache License, Version 2.0 (the “License”);

you may not use this file except in compliance with the License.

You may obtain a copy of the License at

http://www.apache.org/licenses/LICENSE-2.0

Unless required by applicable law or agreed to in writing, software

distributed under the License is distributed on an “AS IS” BASIS,

WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.

See the License for the specific language governing permissions and

limitations under the License.

^{XD021 | © Copyright 2020–2022 Xilinx, Inc.}