Internal Design of MCEuropeanHestonEngine

Overview

The European option is an option that can only be exercised at the expiration date. Heston Model is the most classic model for stock price. This engine uses a large number of random samples to simulate stock price’s dynamic based on Heston Model, then calculates the value of option which use this stock as underlying asset.

Implementation

This engine uses the framework of Monte Carlo Simulation in L1. It has a template argument to setup unroll number of Monte Carlo Module (MCM). For a single MCM, it has two normally distributed random number generators (RNGs) as input, to simulate random walks of stock price and its volatility. Two RNGs will send two random numbers stream to Heston PathGenerator for calculating the stock price at each time steps. The stock price is sent to the pricer for calculating the option’s value of each path. After certain number of paths being generated, the accumulator determines whether the value of options has been “stable” according to its variance. Then, it will stop and output the average of option values as the final result. However, if it is not stable, MCM will move to the next round of calculation to generate more paths.

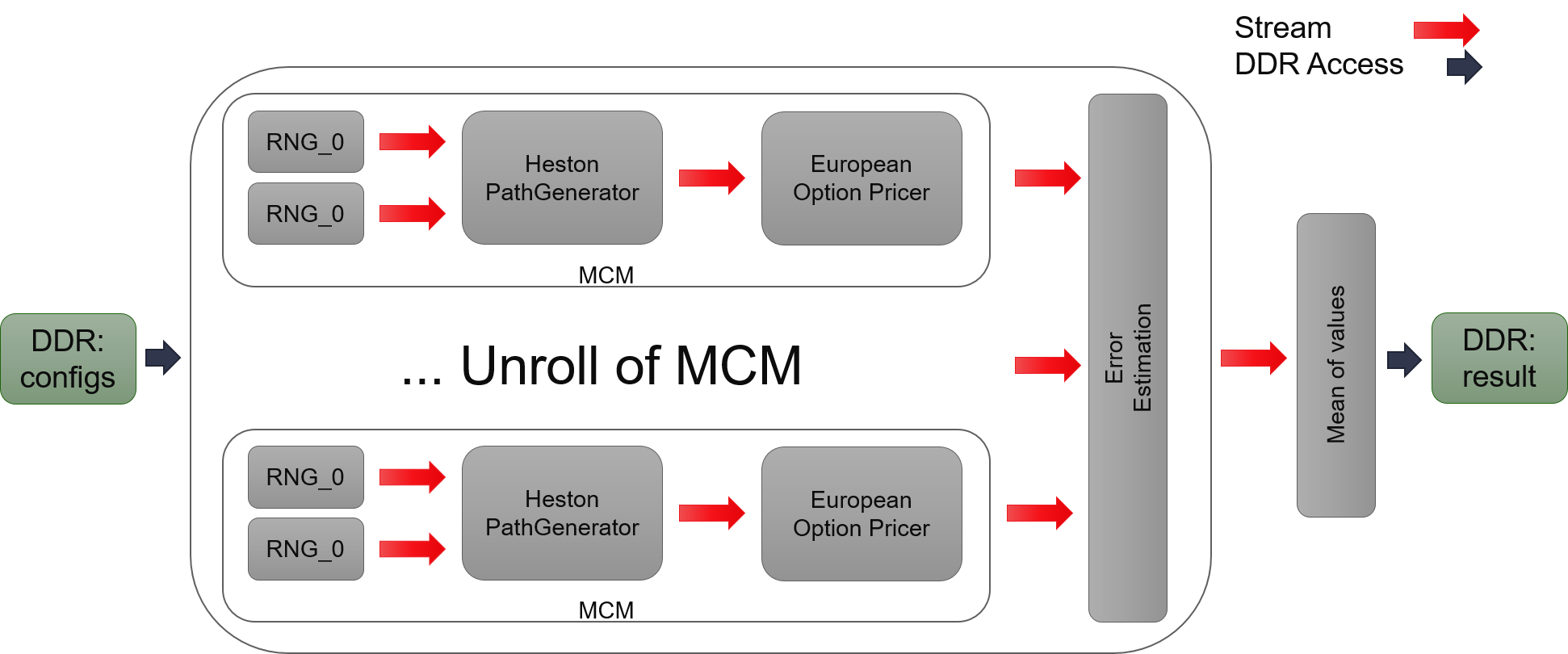
Optimization in two parts:

• 1. Optimization of L1 functions.
• 2. Save one call of cumulative distribution function in single underlying assets since it can get the value directly from RNGs. It may not work for multiple underlying assets because it will lose direct link between Gaussian random number and its corresponding uniform random number.

Variations

In this release we provide five variations of Heston Model implementation, including kDTFullTruncation, kDTPartialTruncation, kDTReflection, kDTQuadraticExponential and kDTQuadraticExponentialMartingale. The first three are relatively simple when dealing with negative volatility. kDTQuadraticExponential and kDTQuadraticExponentialMartingale use a better approximation method to get results with higher precision while taking more resource.