Xilinx Louvain Modularity Alveo Product Overview

Louvain Algorithm

Louvain modularity(Q) is defined as a value in the range [−1/2, 1] that measures the density of links inside communities compared to links between communities. For a weighted graph, modularity is defined as:

where

• Aij represents the edge weight between nodes i and j

• ki and kj are the sum of the weights of the edges attached to nodes i and j, respectively

• m is the sum of all of the edge weights in the graph

• ci and cj are the communities of the nodes

• δ is Kronecker delta function δ(x,y) = 1 if x=y, 0 otherwise

The Louvain algorithm is a hierarchical clustering algorithm, that recursively merges communities into a single node and executes the modularity clustering on the condensed graphs. The figure below illusrates final detected communites with 3 levels after the modularity value is maximized.

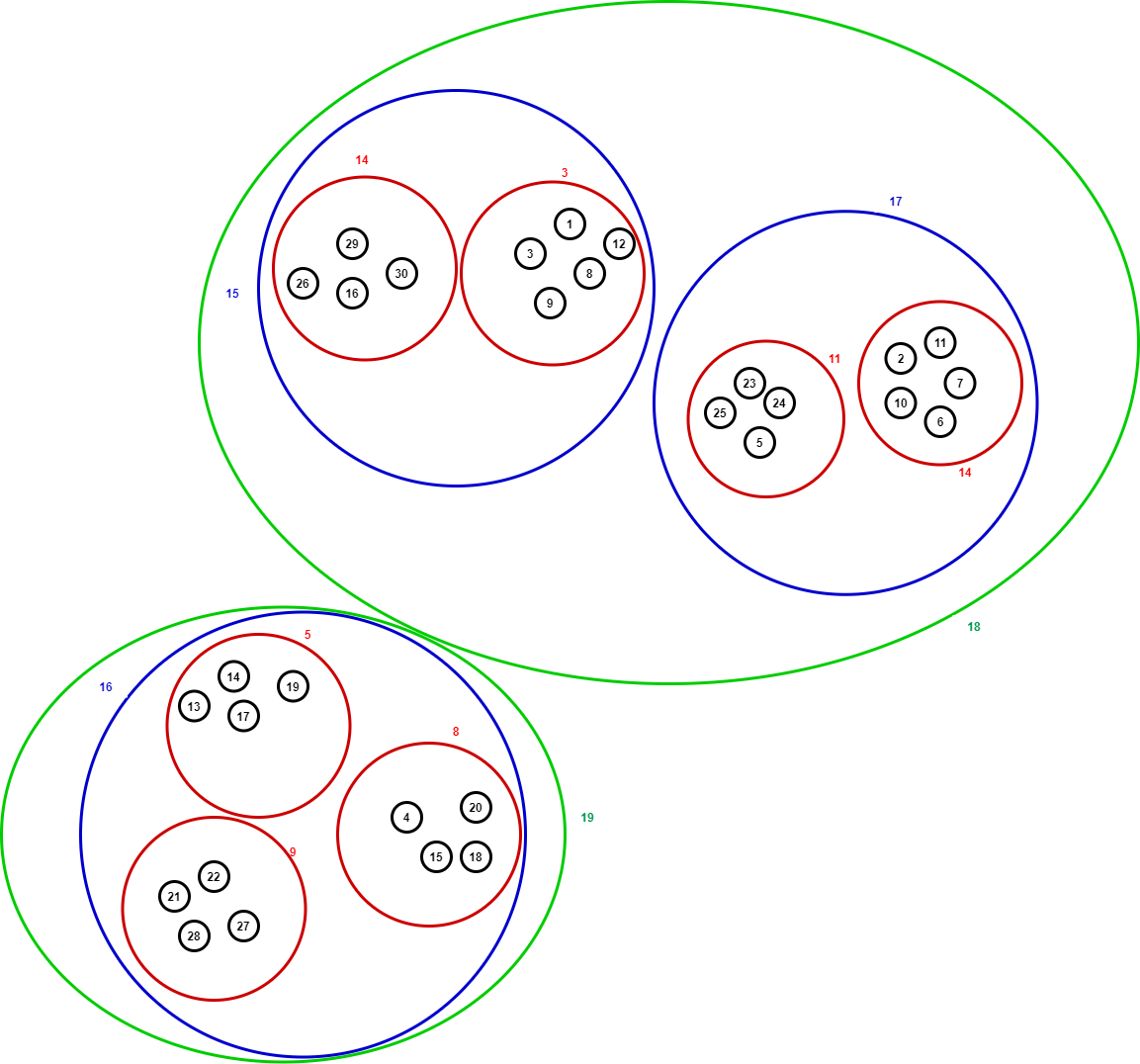
Xilinx Louvain Modularity product running on Xilinx Alveo acceleration cards greatly reduces the compuation time of the modularity value (Q) and memory footprint.

Use cases

Louvain Modularity have been utilized in the following cases:

• Fraud ring detection

• Understand social structure in social networks

• Product or article recommendation