Internal Design of Tree Lattice¶
Overview¶
Tree Lattice is among the most commonly used tools to price options in financial mathematics. In general, the approach is to divide time from now to the option’s expiration into N discrete periods. At the specific time n, the model has a finite number of outcomes at time n + 1 such that every possible change in the state of the world between n and n + 1 is captured in a branch. This process is iterated until every possible path between n = 0 and n = N is mapped. Probabilities are then estimated for every n to n + 1 path. The outcomes and probabilities flow backwards through the tree until a fair value of the option today is calculated (from wikipedia) .
Implemention¶
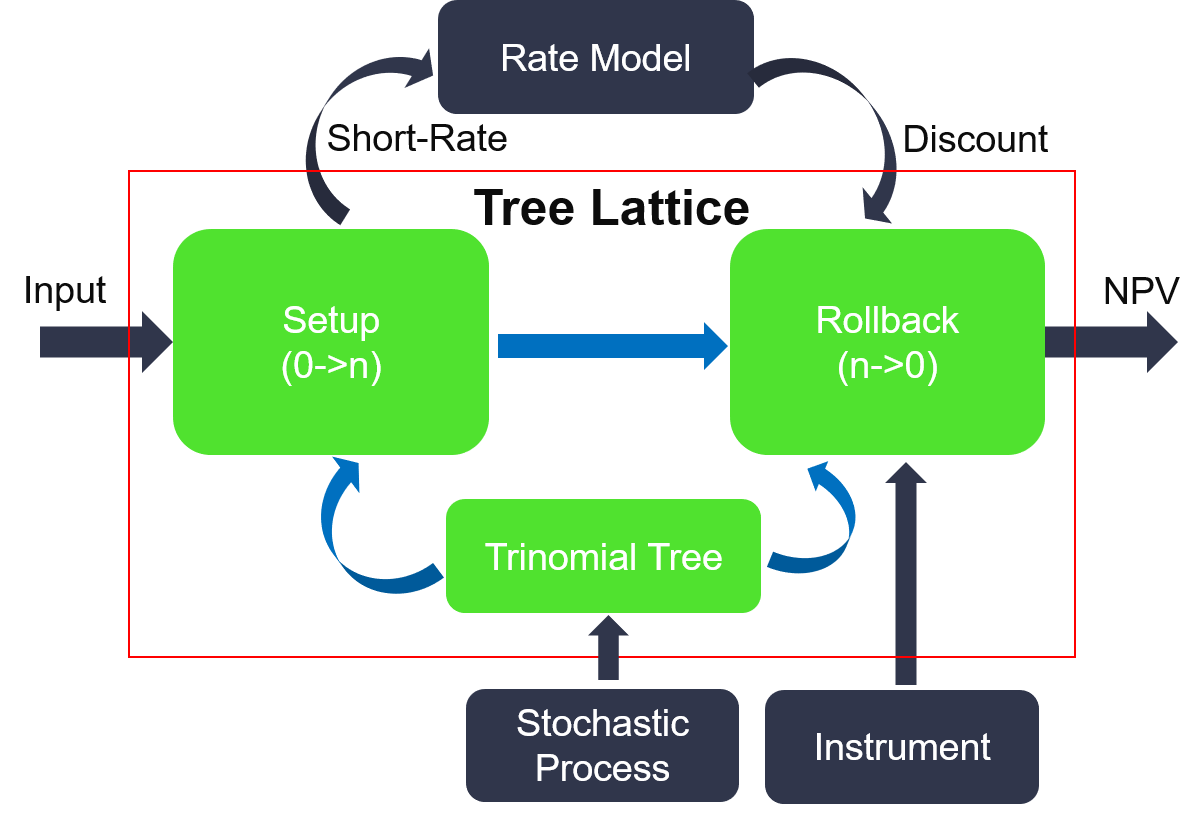
This framework in L1 as shown in Figure 1 that is a trinomial tree based lattice, where the Rate Model supports multiple models including Vasicek, Hull-White, Black-Karasinski, CoxIngersollRoss, Extended-CoxIngersollRoss, Two-additive-factor gaussian, also instruments including swaption, swap, capfloor, callablebond. The process is shown as follows:
- The Setup module of the framework is based on the structure of the tree and Interest Rate Model, and the floating interest rates and tree related parameters are calculated from \(0\) to \(N\) point-by-point to prepare the interest rates and the tree related parameters for the following calculations. To save the on-chip RAM resources, we simply store intermediate results (e.g. \(probs\), \(index\), \(size\), and so on) of single time-point instead all of them from each time points, because they can be directly calculated using the adjacent ones.
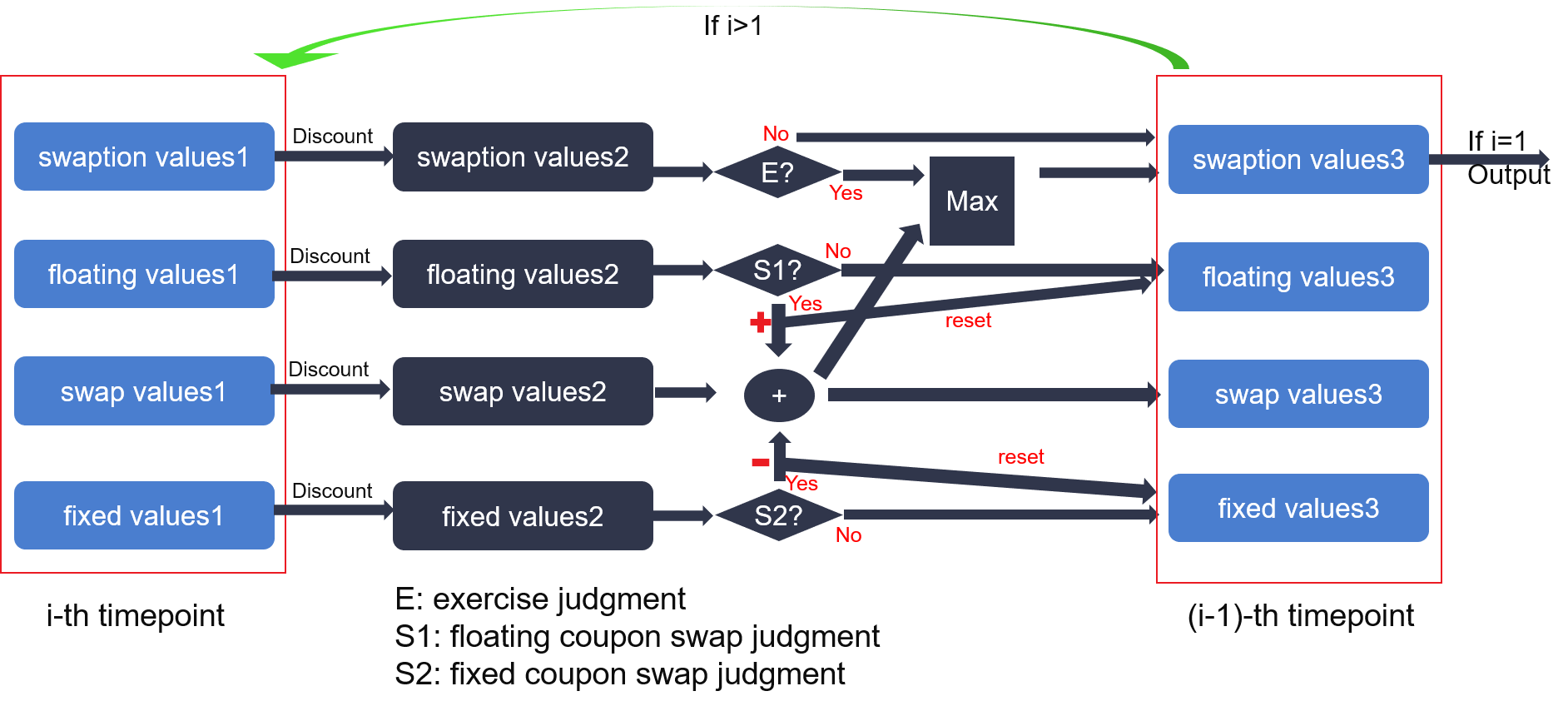
- The Rollback module uses the same structure of the tree and discount functions from the Rate Model to obtain the values of each tree node at the opposite direction. When the time point is 0, the NPV is achieved. The implementation is shown in Figure 2, where the data flows along with the arrows.