AES Decryption Algorithms¶
AES-128/192/256 decryption algorithms processes cipher data blocks of 128 bits, generates plain data blocks of 128 bits using same cipher keys of 128/192/256 bits in data encryption. Basic unit of AES algorithms operation is a two dimensional array of 16 bytes called states. Its mapping relation is as illustrated in the figure below.

Original Implementation¶
Similarly, AES decryption consists of 5 part: KeyExpansion, Inverse SubBytes, Inverse ShiftRows, Inverse MixColumns and AddRoundKey.
KeyExpansion also generates 11/13/15 round keys from input cipher key and they maps to 2-D array as states do.
For one input cipher block, AES-128/192/256 decryption performs 10/12/14 round of processing with the former round keys from behind, each at a time. Thus, input cipher data blocks will operate XOR with the last roundkey. After that, every round sequentially goes through AddRoundKey, Inverse MixColumns, Inverse ShiftRows and Inverse SubBytes. Meanwhile, Inverse MixColumns will be bypassed at the first round.
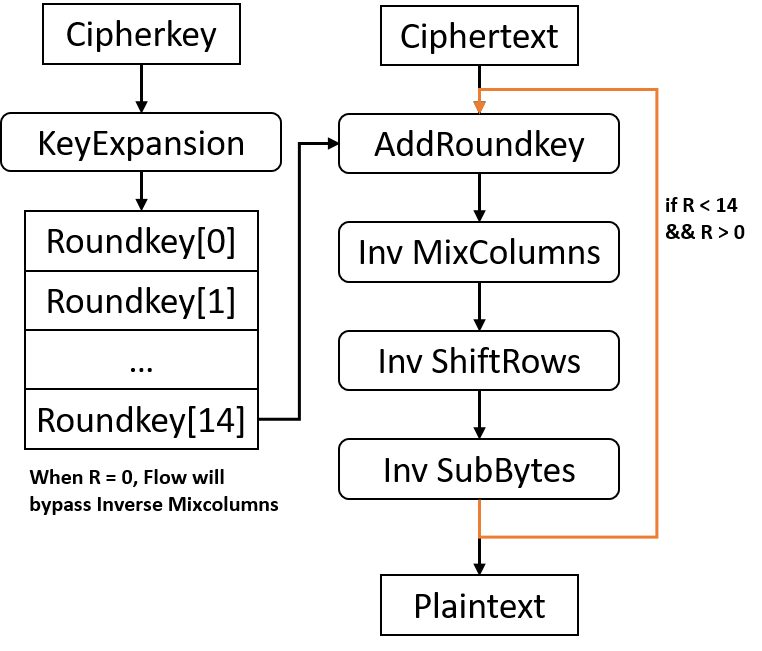
Like AES encryption, Inverse SubBytes are transformed into looking up table which is called inverse S-box and is different with that in encryption. Details can be found in the chapter of AES encryption.
During Inverse ShiftRows, right circular shift are operated based on each row number in 2-D state array.
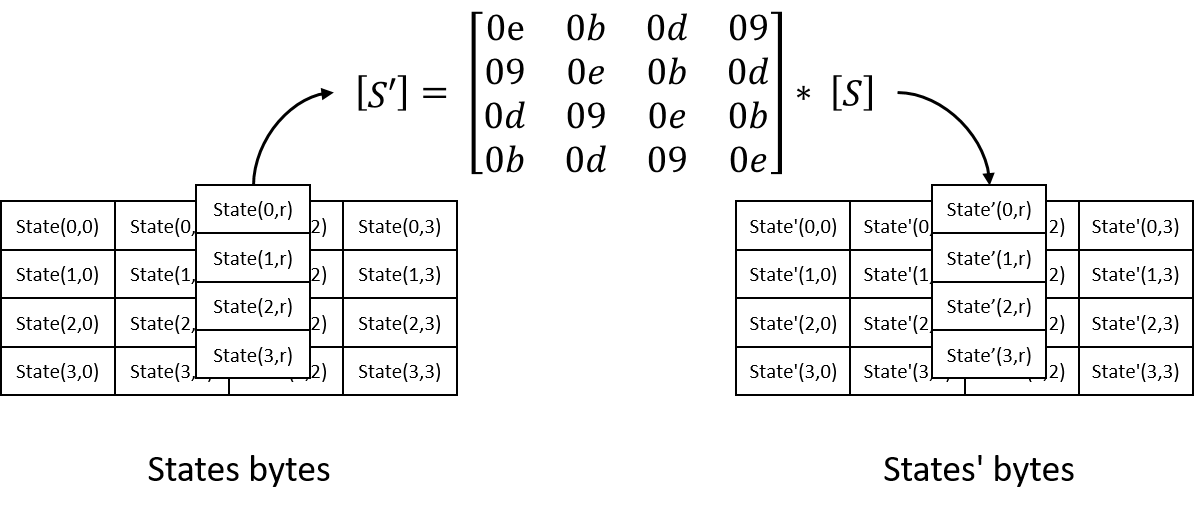
In Inverse MixColumns step, matrix multiplication is involved to transform each column of states. Transform matrix is fixed and calculation treats each bytes as polynomials with coefficients in GF(2^8), modulo x^4 + 1.
In AddRoundKey step, states in each column operate XOR with roundkey of this round.
Optimized Implementation on FPGA¶
Like in AES encryption, we separate key expansion away from decryption. We must call updateKey() before use a new cipher key to decrypt message.
Based on similar consideration in AES encryption implementation, we also can merge inverse SubBytes and Inverse MixColumns into one look-up table as long as operation flow is re-ordered appropriately. Therefore, we adopt that Inverse MixColumns and AddRoundKey are exchanged with each other in one operation round. However, generated key at KeyExpansion stage must be followed by one extra Inverse MixColumns operation for correct decryption. It’s worth to do because of hardware overhead of matrix multiplication in GF(2^8) will be reduced obviously. Furthermore, this addition operation will be executed only once for most case which plenty of blocks are decrypted with sharing the same cipher key. The optimzed flow is shown as below.
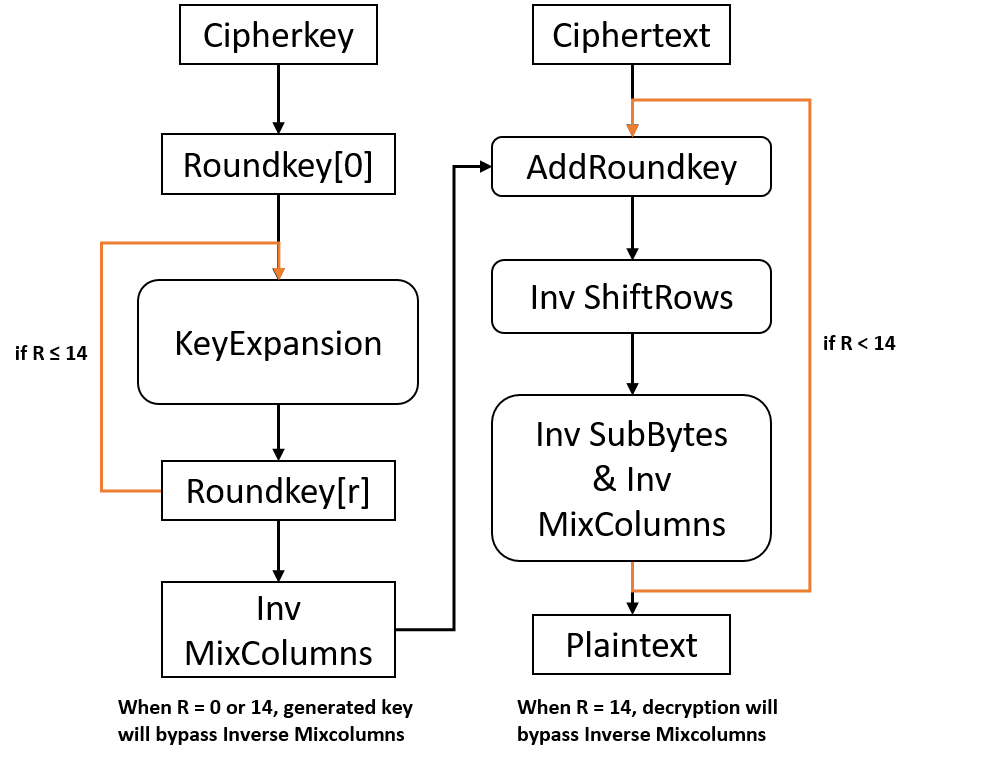
Since each round of process needs one round key in reverse order, and that indicateds the dependency between KeyExpansion and decryption process. KeyExpansion is separated from the whole decryption loop.
In addition, in order to eliminate unnecessary inverse SubBytes operation in the common loop-up table within decryption process, one same SubBytes process should be operated on round keys before they come into Inverse MixColumns step. For the last round in one block decryption, Inverse MixColumns will be skipped.
AES-128 Decryption Performance (Device:U250)¶
| II | CLB | LUT | FF | DSP | BRAM | SRL | URAM | CP(ns) |
|---|---|---|---|---|---|---|---|---|
| 1 | 5305 | 27673 | 11074 | 0 | 10 | 710 | 0 | 3.076 |
AES-192 Decryption Performance (Device:U250)¶
| II | CLB | LUT | FF | DSP | BRAM | SRL | URAM | CP(ns) |
|---|---|---|---|---|---|---|---|---|
| 1 | 6409 | 33433 | 13296 | 0 | 14 | 898 | 0 | 3.032 |
AES-256 Decryption Performance (Device:U250)¶
| II | CLB | LUT | FF | DSP | BRAM | SRL | URAM | CP(ns) |
|---|---|---|---|---|---|---|---|---|
| 1 | 7442 | 38636 | 14985 | 0 | 10 | 1153 | 0 | 3.016 |