AES Encryption Algorithms

AES-128/192/256 Algorithm process plain data blocks of 128 bits, generates cipher data blocks of 128 bits using cipher keys of 128/192/256 bits. Basic unit of AES algorithms operation is a two dimensional array of 16 bytes called states. Its mapping relation is as illustrated in the figure below.

Original Implementation

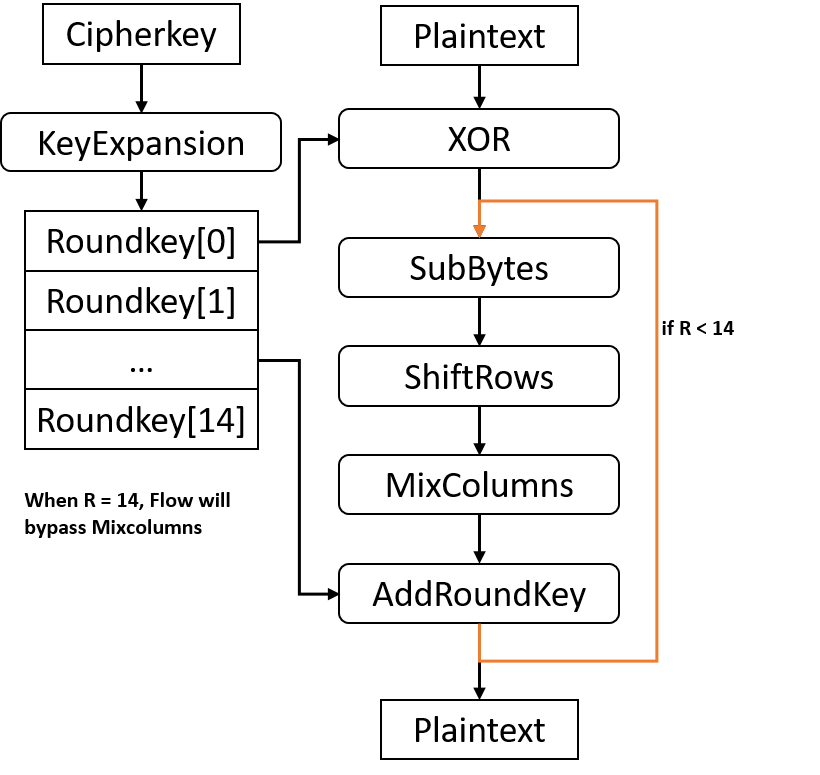
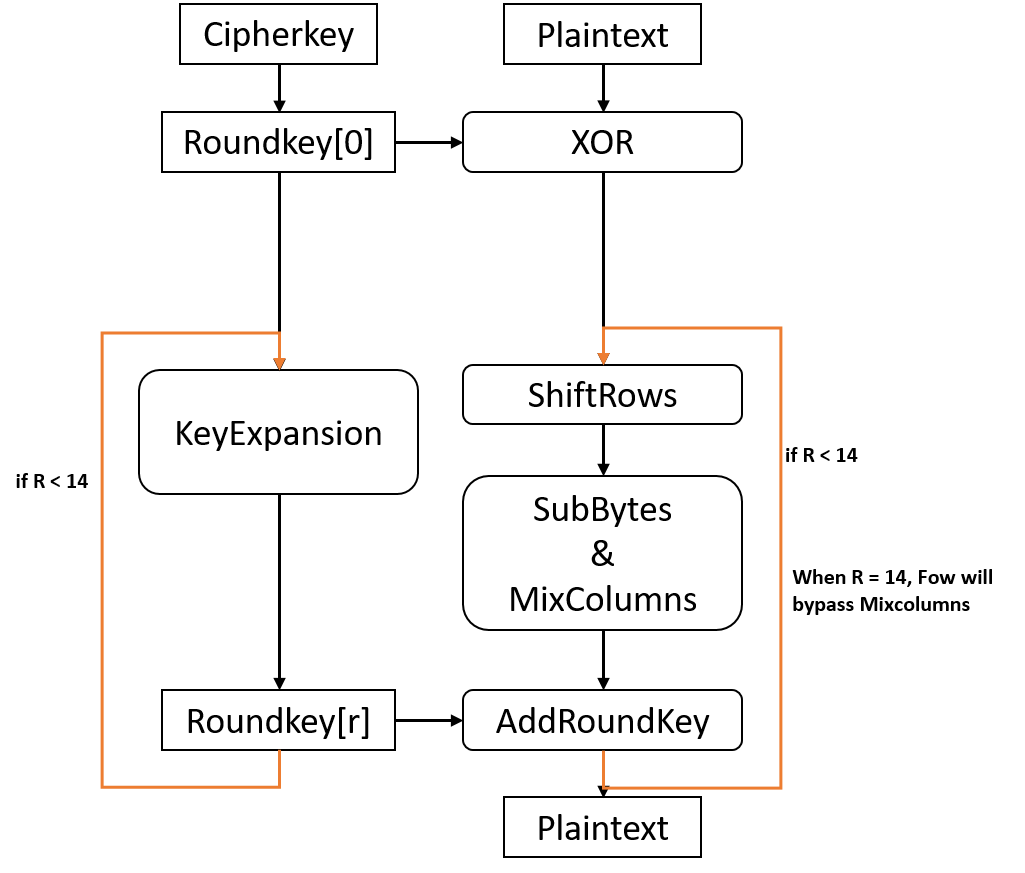
AES-128/192/256 encryption consist of 5 part: KeyExpansion, SubBytes, ShiftRows, MixColumns and AddRoundKey.

KeyExpansion generates 11/13/15 round keys from original cipher key and they maps to 2-D array as states do.

AES encryption first does XOR add to input plain data blocks with first roundkey. Then AES-128/192/256 encryption performs 10/12/14 round of processing with the left round keys, each at a time. Each round sequentially does SubBytes, ShiftRows, MixColumns and AddRoundKey.

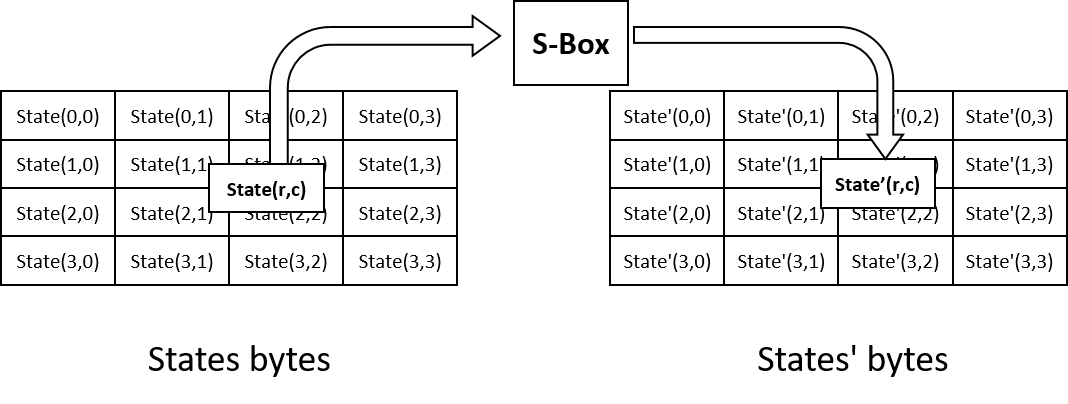
During SubBytes, each bytes of states is transformed by looking up table S-box using their value as address.

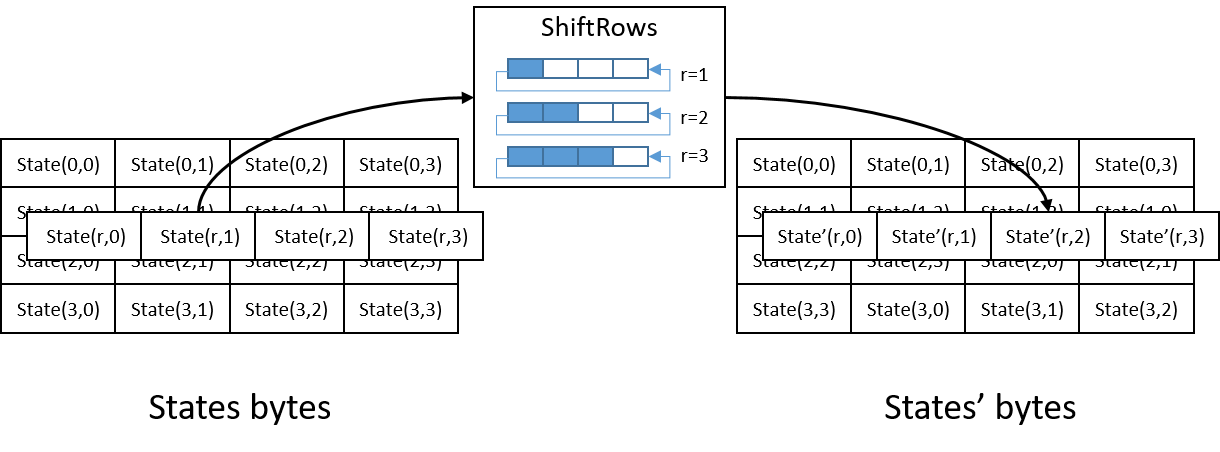
During ShiftRows, last 3 rows of states are cyclically shifted over different number of bytes based on row number.

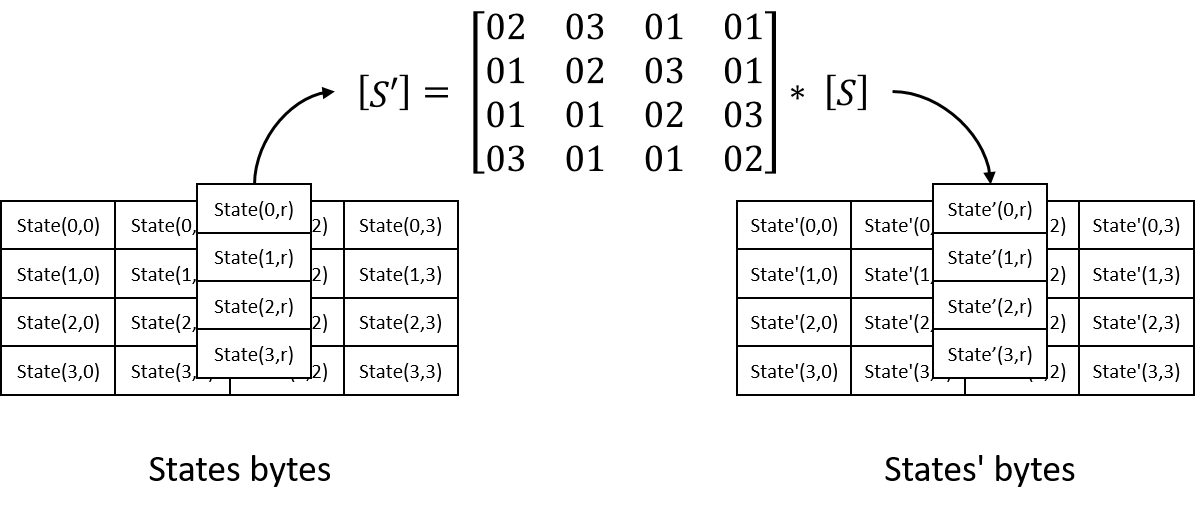
During MixColumns, perform operation on each column of states. Basically it use matrix multiplication to transform each column of states. Transform matrix is fixed and calculation treats each bytes as polynomials with coefficients in GF(2^8), modulo x^4 + 1.

During AddRoundKey, states are XOR with roundkey of this round.

Optimized Implementation on FPGA

We seperate key expansion away from encryption. Which means we have to call updateKey() before using a new cipher key to encrypt message.

Because SubBytes is independent of each byte’s location in states and ShiftRows only shifts in integer of bytes, these two part could exchange their position in processing sequence without changing the result. Although no improvement is achieved here, this will benefit later optimization.

The matrix multiplication in MixColumns is actually two parts: multiply bytes in column of states with bytes in row of the matrix, then add the result. Value of matrix elements could only be 01, 02 or 03. We can get the original result of SubBytes and its multiplication of 01, 02 or 03 by one-time’s look up of a new S-Box table called “sbox_mix_col_1”. This could save a lot of logics to do multiplication.

Based on similar consideration, we also merge such multiplication in KeyExpansion into one time table look up of another new S-Box called “sbox_Rcon”. Although sbox_Rcon and sbox_mix_col_1 are bigger than original S-Box, they all could be stored in 1 BRAM on chip. Such merges saves logics without additional resource cost.

AES-128 Encryption Performance (Device: U250)

II	CLB	LUT	FF	DSP	BRAM	SRL	URAM	CP(ns)
1	2069	9109	7169	0	2	642	0	2.560

AES-192 Encryption Performance (Device: U250)

II	CLB	LUT	FF	DSP	BRAM	SRL	URAM	CP(ns)
1	2725	13321	8917	0	6	898	0	2.976

AES-256 Encryption Performance (Device: U250)

II	CLB	LUT	FF	DSP	BRAM	SRL	URAM	CP(ns)
1	3041	15112	10619	0	2	1153	0	2.794