Internals of Insert Sort¶
This document describes the structure and execution of Insert Sort, implemented as insertSort function.
Principle¶
Insert sort is a simple sorting algorithm that builds the final sorted array (or list) one item at a time. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort. However, insert sort provides several advantages:
1.Simple implementation;
2.Efficient for (quite) small data sets, much like other quadratic sorting algorithms;
3.The time complexity is O(nk) when each element in the input is no more than k places away from its sorted position;
4.Only requires a constant amount O(1) of additional memory space;
5.Sort a list as it receives it.
For its FPGA implementation, a dedicated structure is designed as follow:
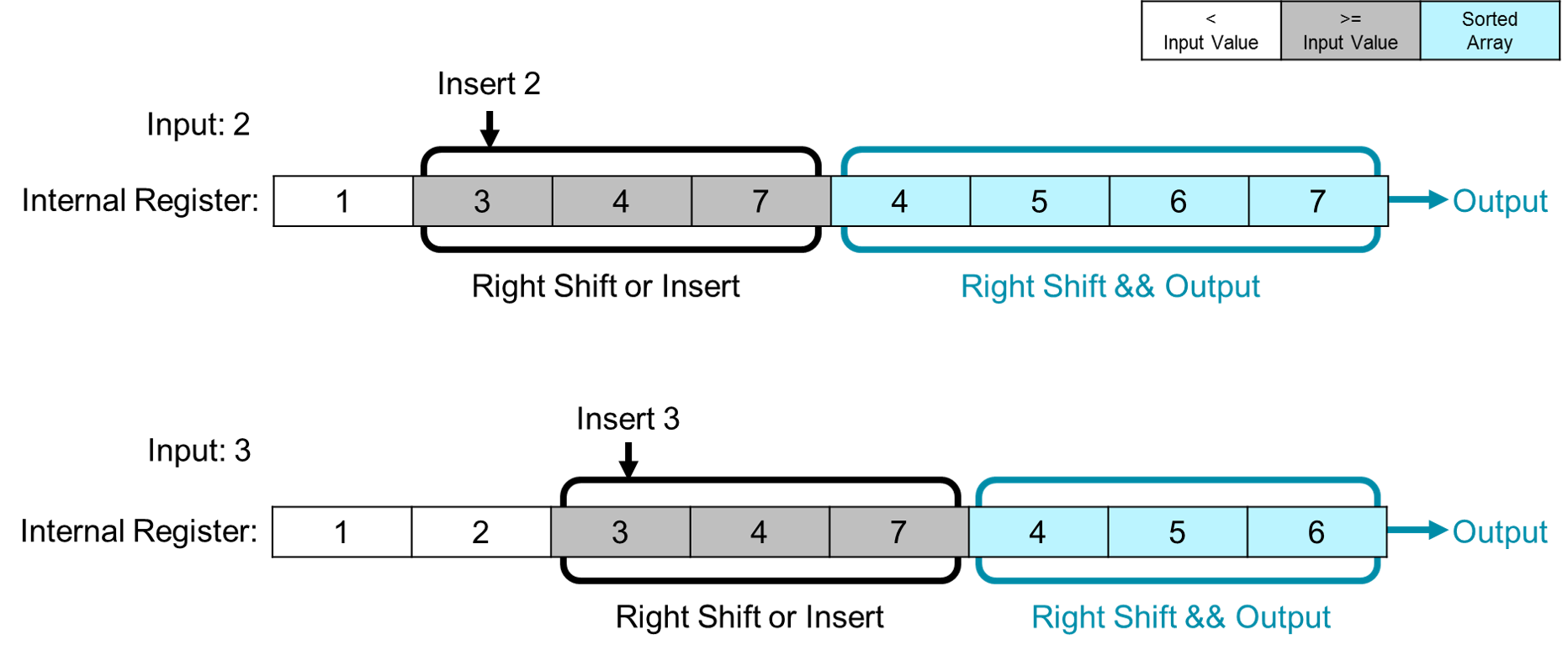
The Insert Sort primitive has an internal shift register array to sort the input stream. It takes five steps to finish the sort processing of a stream with limited max sort number.
1.Build a group of shift registers, and the number of shift register is the maximum sort number;
2.Broadcasting the input value to every shift registers, then comparing size between the internal value of each shift register and the input value. For descending sort, run step3. Otherwise, run step4;
3.For descending sort, we should build a internal ascending array. If the input value is larger than array[i], then right shift array[i]. If the input value is less than array[i] and larger than array[i+1], insert input value to array[i+1];
4.For ascending sort, we should build a internal descending array. If the input value is less than array[i], then right shift array[i]. If the input value is larger than array[i] and less than array[i+1], insert input value to array[i+1];
5.If input stream is not empty, output the last value of the array and then return to step2. Otherwise, right shift the whole register array and output the last array value until the array is empty.
Synthesis Results¶
For bitwidth=32, the resource consumption for different max sort number is listed in the table below:
| Max_sort_number | 8 | 16 | 32 | 64 | 128 | 256 | 512 |
| Interval | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| LUT | 343 | 607 | 1135 | 2144 | 4192 | 8285 | 16477 |
| Register | 1007 | 1835 | 3451 | 6692 | 13156 | 26082 | 51885 |
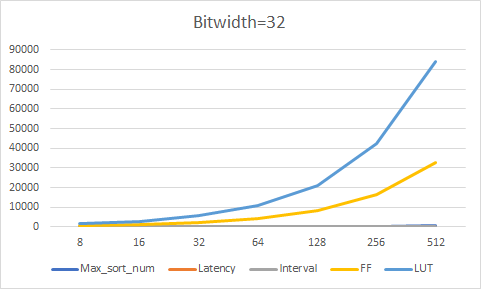
Insert Sort primitive set 1024 as the default maximum sort number. In order to achieve arbitrary sort number, firstly the input stream will be sorted every 1024 number by Insert Sort primitive, then we use Merge Sort primitive to merge the sorted stream, see reference Internals of Merge Sort. The picture below show the synthesis result for maximum sort number of 1024.


Implementation Results¶
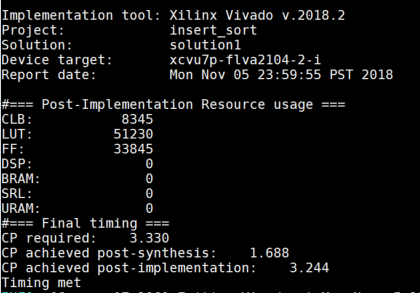
This is the implementation result of Insert Sort primitive with Max_sort_number=1024:
Important
The max sort number should be less than 1024 because array partition can only support array size smaller then 1024. For arbitary sort number, Merge Sort primitive is required Internals of Merge Sort
Caution
The size of input stream should be larger than the max sort number, otherwise the internal shift register is not fully initialized.
This insertSort primitive has one port for key input, one port for payload input, one port for key output, one port for payload output and one boolean sign for indicating ascending sort or descending sort.