Singular Value Decomposition for general matrix (GESVJ)¶
Overview¶
One-sided Jacobi alogirhm is a classic and robust method to calculate Singular Value Decompositon (SVD), which can be applied for any dense matrix with the size of \(M \times N\). In this library, it is denoted as GESVJ, same as the API name used in LAPACK.
where \(A\) is a dense symmetric matrix of size \(m \times n\), \(U\) is \(m \times m\) matrix with orthonormal columns and and \(V\) is \(n \times n\) matrix with orthonormal columns, and \(\Sigma\) is diagonal matrix. The maximum matrix size supported in FPGA is templated by NRMAX, NCMAX.
Algorithm¶
The calculation process of one-sided Jacobi SVD method is as follows:
- Initialize matrix V = I
- Select two columns (i, j), i < j, of matrix A, namely \(A_i\) and \(A_j\). Accumulate two columns of data by fomular
A \(2 \times 2\) matrix can be obtained and noted as:
where \(b_{ij}\) equals \(b_{ji}\).
- Solve the \(2 \times 2\) symmetric SVD with Jacobi rotation:
if we put s and c in a matrix as J, then J equals
- Update the i and j columns of matrix A and V by
- Calculate converage of \(2 \times 2\) matrix by
and select the max converage of all pairs (i, j).
- Repeat steps 2-4 until all pairs of (i, j) are calculated and updated.
- If the max converage among all paris of (i, j) is bigger than 1.e-8, repeat steps 2-6 again, which is also called one sweep.
- When the converge is small enough, calculate the matrix U and S for each \(i = 1, ..., n\) by
Architecture¶
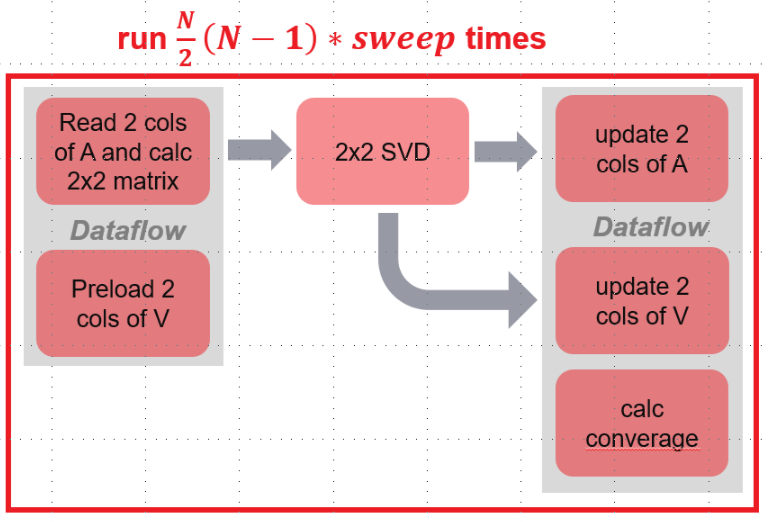
From the algorithm, we know that the core part of the computation is two columns of data read-and-accumulate, and then updating corresponding two columns of data in Matrix A and V. In this library, we implement this core module in the following architecture.
It can be seen from the architecture, steps 2-5 (each pair of i and j) of the algorithm is divided into three stages:
- Stage 1:
- read two columns of data of A to BRAM and accumulate to \(b_{ii}\), \(b_{jj}\) and \(b_{ij}\).
- preload two columns of data of matrix V to BRAM.
- Stage 2:
- Calculate SVD for \(2 \times 2\) matrix
- Stage 3:
- Update two columns of data in matrix A
- Update two columns of data in matrix V.
- Meanwhile, calculate converage for current pair (i, j).
Since operating data of matrix A and V are independent, two modules of stage 1 are running in parallel. Meanwhile, thress modules of stage 3 run in parallel. The last module of stage 3 calculates converage using \(2 \times 2\) matrix data. This converage computing process is in read-and-accu module of stage 1 according to the algorithm. However, it requires ~60 cycles, which is also a lot after partitioning matrix A by row. Therefore, this calculation process is extracted as a submodule in stage 3.
Note
Why updating matrix V is divided into two modules?
From the figure, we can see that there are two modules related to matrix V, preload two columns of data of V to BRAM, and updating V. In our design, matrix A and V are all saved in URAM. And for each URAM, only 2 ports of read/write are supported. Since matrix A cummulated \(2 \times 2\) data need 100+ cycles to do SVD. We may preload two columns of V into BRAMs via 2-reading ports of URAM. And using two writting ports when updating data in V.
Besides, in order to speed up the data reading and updating of matrix V data, the matrix V is partitioned by NCU through its row. For each CU, matrix V is read/written using 2 URAM ports.
Note
Supported data size:
The supported maximum size of matrix A that templated by NRMAX and NCMAX is 512. The partitioning number MCU and NCU can support up to 16, respectively.