Supply Chain Optimization Overview¶
The supply chain optimization problem can be formulated as a travel plan scheduling problem utilizing the power of TigerGraph Graph database in the following way.
Consider a list of travel plans or trips that need to be completed. Additionally, consider two types of resources (1) Trucks and (2) Work Orders, that are used to execute a travel plan. The use case is constrained by the following specifications:
There are a fixed number of trucks
Each travel plan is assigned a truck (not necessarily unique)
Number of trucks << Number of travel plans
There are a fixed number of work orders to be completed
Each travel plan is associated with one or more work orders
A work order might need more than 1 trip to be completed
Number of work orders << Number of travel plans
Finally, the resource conflict is modelled as:
If two travel plans share a truck or a work order, they can not be executed at the same time.
Problem Formulation¶
In this example, the goal is to execute all travel plans in the least amount of time. To accomplish this, it can be stated that for a list of travel plans that are yet to be scheduled, we need to find the maximum number of travel plans that can be scheduled at the same time, given the set of available trucks and work orders to complete. When a set of scheduled travel plans are finished, the process is repeated until all travel plans are executed.
Travel plans, trucks, work orders and their relationships can be easily captured by creating a TigerGraph graph database. Consider a scenario with 3 travel plans, 2 trucks and 2 work orders. The travel plans have dependencies on trucks and work orders as shown in the following figure:
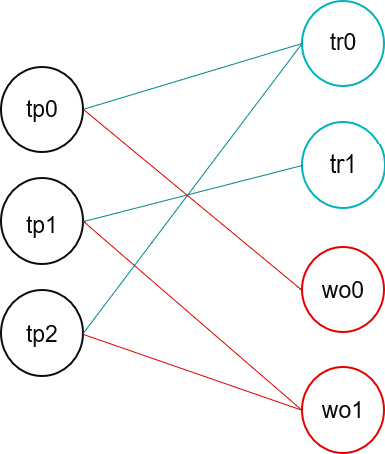
Truck tr0 is used in trips tp0 and tp2 while truck tr1 is used only in trip tp1. Similarly, work order wo0 is part of only trip tp0 while work order wo1 is split between trips tp1 and tp2. These dependencies create conflicts such that travel plans tp0 and tp2 can not be executed at the same time. This relationship is captured in a travel plans conflict graph as shown below where travel plans are represented as vertices and are connected by an edge if there is a schedule conflict between them.
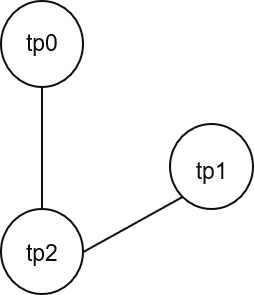
TigerGraph allows creation of the conflict graph easily by writing queries in GSQL. New edges are created in the original graph so that traversal can be done only on travel plan to travel plan edges while computing the MIS.
MIS Formulation¶
After a conflict graph is obtained like above, the supply chain optimization problem can be modelled as an MIS problem on the conflict graph: Given the conflict graph of travel plans yet to be scheduled, find the MIS of the graph to obtain set of travel plans that can be scheduled at the same time. Execute the obtained MIS travel plans, remove vertices and edges associated to them from the conflict graph, and run MIS on the remaining sub-graph. This is continued till the graph is empty.
If a maximal set is used instead of the maximum set, the scheduling will not be optimal. The Xilinx Maximal Independent Set library produces high “quality” (close to maximum) sets which can achieve close to optimal results for all practical purposes.