Linear Regression (Predict)¶
Linear Least Square Regression¶
Linear Least Square Regression is a model to predict a sample’s scalar response based on its features. Its prediction prediction function’s output is linear to samples:
LASSO Regression¶
LASSO Regression in prediction is the same with linear least square regression. Its major difference against linear least square is training stage.
Ridge Regression¶
Ridge Regression in prediction is the same with linear least square regression. Its major difference against linear least square is training stage.
Implementation (inference)¶
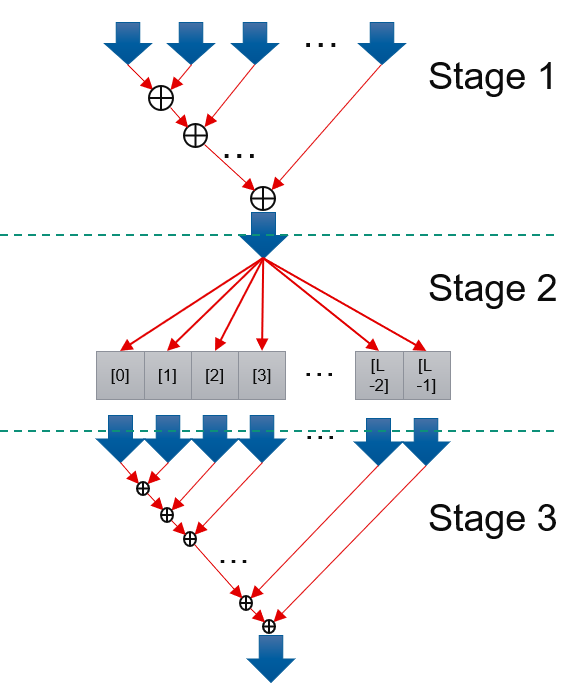
Input of predict function are D streams of features, in which D is how many features that predict function process at one cycle. According to prediction model formular, to calculate final result, it has dependency issue. In order to achieve II = 1 to process input data, prediction comes in three stage. Stage 1: Compute sum of D features multiply D weights, name it as partSum. Later D features’ processing does not depend on former D features. It could achieve II = 1. Stage 2: Compute sum of partSum, we allocate a buffer whose length(L) is longer than latency of addition, and add each partSum to different position. 0th partSum will be add to 0th buff, 1st to 1st buff… The L th part Sum will be added to 0th buff. Because L is longer than addition latency, the 0th buff has already finished addition of 0 th buffer. So L th partSum’s addition won’t suffer dependency issue. So Stage 2 could Archieve II = 1. Stage 3: Add L buffs and get final result. This part also does not have dependency issue and could achieve II = 1. Stage 1 - 3 are connected with streams and run dataflow. In this way, we could achieve II = 1 in total.
The correctness of Linear Regression/LASSO Regression/Ridge Regression is verified by comparing results with Spark mllib. The results are identical.