Logistic Regression (Predict)¶
Logistic Regression Classifier¶
Logistic Regression is a model to label a sample with integer from 0 to L - 1 in which L is class number. For a L class label, it needs L - 1 vector to calculate L - 1 margins. Its formula is shown as below. Its prediction prediction function’s output is linear to samples:
Then label is decided according to L - 1 margins based on formula below.
Implementation (inference)¶
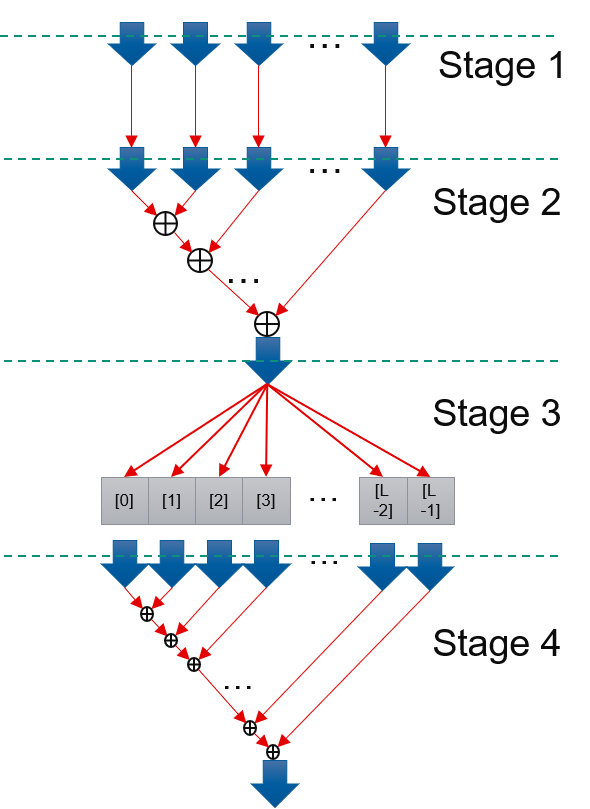
Input of predict function are D streams of features, in which D is how many features that predict function process at one cycle. According to prediction model formular, to calculate final result, it has dependency issue. In order to achieve II = 1 to process input data, prediction comes in four stage. Stage 1: Read D features in one cycles and repeat them (L - 2 + K) / K times. Stage 2: Compute sum of D features multiply D weights, name it as partSum. Later D features’ processing does not depend on former D features. It could achieve II = 1. Stage 3: Compute sum of partSum, we allocate a buffer whose length(L) is longer than latency of addition, and add each partSum to different position. 0th partSum will be add to 0th buff, 1st to 1st buff… The L th part Sum will be added to 0th buff. Because L is longer than addition latency, the 0th buff has already finished addition of 0 th buffer. So L th partSum’s addition won’t suffer dependency issue. So Part 3 could Archieve II = 1. Stage 4: Add L buffs and get final result. This part also does not have dependency issue and could achieve II = 1. Stage 1 - 4 are connected with streams and run dataflow.
The correctness of Logistic Regression is verified by comparing results with Spark mllib. The results are identical.