Internal Design of MCMultiAssetEuropeanHestonEngine¶
Overview¶
Heston Model is the most classic model for stock price. European option is an option that can only be exercised at the expiration date. MCMultiAssetEuropeanHestonEngine aims to calculate pay off of European option whose underlying asset is sum of multiple underlying assets. These assets may influence each other which means their volatility is not independent. We use a matrix to describe their correlations. This engine uses this matrix so calculate random variables that have that correlation. Then it uses large number of random samples to simulate stock prices’ dynamic based on Heston Model. And finally calculates value of option which use these stock as underlying assets.
Implementation¶
This engine is similar to MCEuropeanHestonEngine. The main difference is that it have additional stage to calculate random variables that have certain correlation. Assume there’re \(N\) underlying asset, each asset needs \(2\) random variable, \(2N\) random variable in total. The correlation matrix is and \(2N\) by \(2N\) matrix, but the right upper triangle is all zeros after LU decomposition, leaving only \((2N + 1)N\) non-zero elements. By cutting of none zeros elements, it will save nearly half DSPs to calculate correlated random variables.
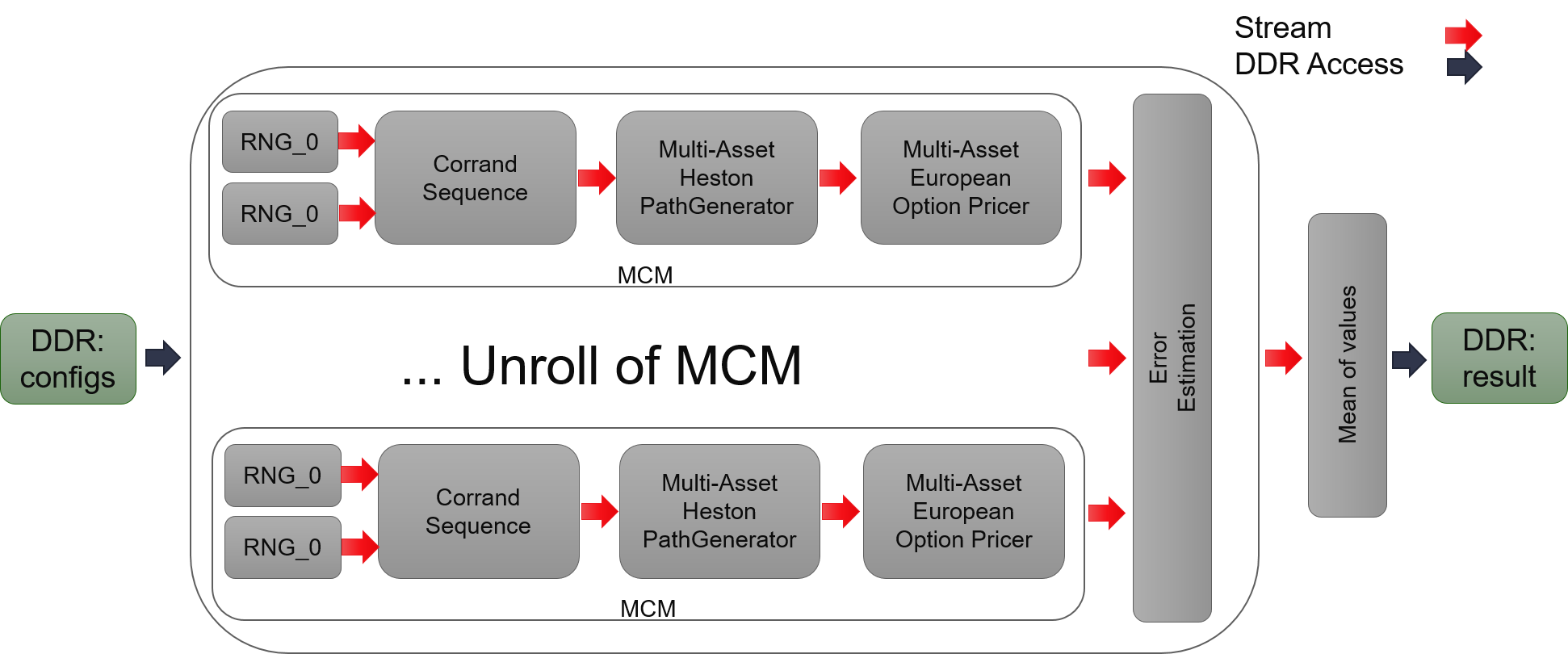
Optimization comes in two parts.
- The first and also the most is optimization of L1 functions.
- Save one call of cumulative distribution function in single underlying assets since it can get the value directly from RNGs. It may not work for multiple underlying assets because it will lose direct link between Gaussian random number and its corresponding uniform random number.
Variations¶
In this release we provide five variations of Heston Model implementation, including kDTFullTruncation, kDTPartialTruncation, kDTReflection, kDTQuadraticExponential and kDTQuadraticExponentialMartingale. The first three is relatively simple dealing with negative volatility. kDTQuadraticExponential and kDTQuadraticExponential Martingale use better approximation method to get result with better precision while taking more resources.