Quantized QuartzNet with Brevitas for efficient speech recognition

27 Mar 2020 - Giuseppe Franco

Although not yet supported in FINN, we are excited to show you how Brevitas and quantized neural network training techniques can be applied to models beyond image classification.

We are pleased to announce the release of quantized pre-trained models of QuartzNet for efficient speech recognition. They can be found at the following link, with a brief explanation on how to test them. The quantized version of QuartzNet has been trained using Brevitas, an experimental library for quantization-aware training.

QuartzNet, whose structure can be seen in Fig. 1, is a convolution-based speech-to-text network, based on a similar structure as Jasper.

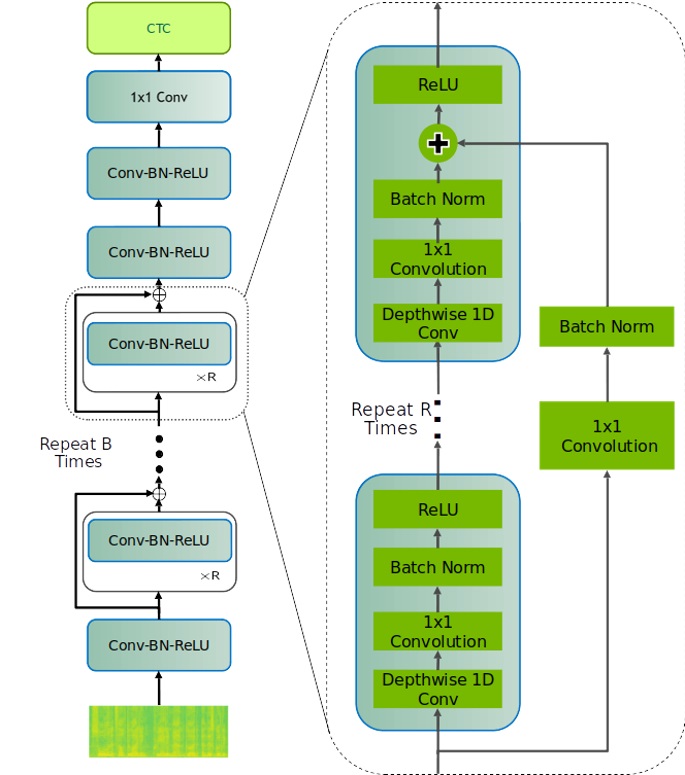Fig. 1 QuartzNet Model, source

The starting point is the mel-spectrogram representation of the input audio file. Through repeated base building blocks of 1D Convolutions (1D-Conv), Batch-Normalizations (BN), and ReLU with residual connections, QuartzNet is able to reconstruct the underlying text. The main difference with respect to Jasper is the use of Depthwise and Pointwise 1D-Conv (Fig. 2a), instead of ‘simple’ 1D-Conv (Fig. 2b). Thanks to this structure, QuartzNet is able to achieve better performance in terms of Word Error Rate (WER) compared to Jasper, using only 19.9 M parameters, compared to 333M parameters of Jasper.

Moreover, the authors proposed a grouped-pointwise convolution strategy that allows to greatly reduce the numbers of parameters, down to 8.7M, with a little degradation in accuracy.

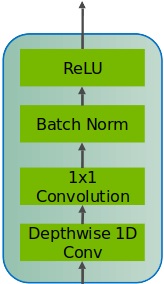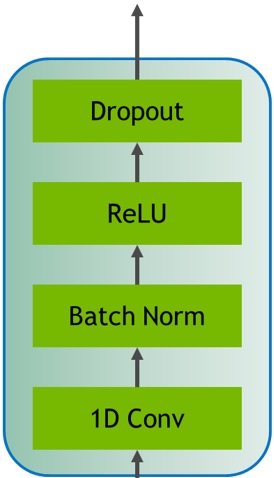Fig. 2a QuartzNet Block, source	Fig. 2b Jasper Block source

The authors of QuartzNet proposes different BxR configurations. Each B_i block consist of the same base building block described above, repeated R times. Different BxR configurations have been trained on several different datasets (Wall Street Journal, LibriSpeech + Mozilla Common Voice, LibriSpeech only).

For our quantization experiments, we focus on the 15x5 variant trained on LibriSpeech with spec-augmentation without grouped convolutions. More detail about this configuration can be found in the paper and on a related discussion with the authors.

Started from the official implementation, the first step was to implement a quantized version of the topology in Brevitas, using quantized convolutions and activations.

After implementing the quantized version, the second step was to re-train the model, starting from the pre-trained models kindly released by the authors.

We focused on three main quantization configurations. Two configurations at 8 bit, with per-tensor and per-channel scaling, and one configuration at 4 bit, with per-channel scaling.

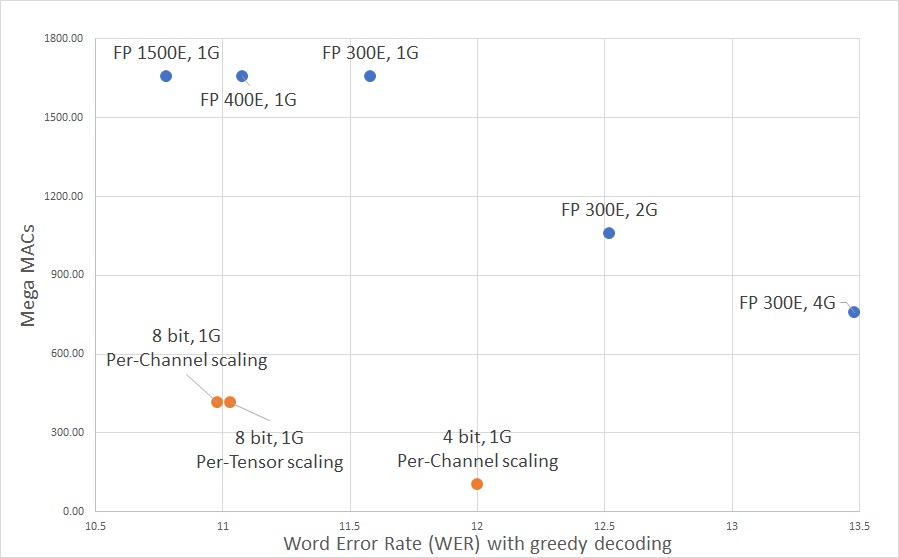
We compare our results with the one achieved by the authors, not only in terms of pure WER, but also the parameter’s memory footprint, and the number of operations performed. Note that the WER is always based on greedy decoding. The results can be seen in Fig. 3 and Fig. 4, and are summed up in Table 1.

Configuration	Word Error Rate (WER)	Memory Footprint (MegaByte)	Mega MACs
FP 300E, 1G	11.58%	37.69	1658.54
FP 400E, 1G	11.08%	37.69	1658.54
FP 1500E, 1G	10.78%	37.69	1658.54
FP 300E, 2G	12.52%	24.06	1058.75
FP 300E, 4G	13.48%	17.25	758.86
8 bit, 1G Per-Channel scaling	10.98%	18.58	414.63
8 bit, 1G Per-Tensor scaling	11.03%	18.58	414.63
4 bit, 1G Per-Channel scaling	12.00%	9.44	104.18

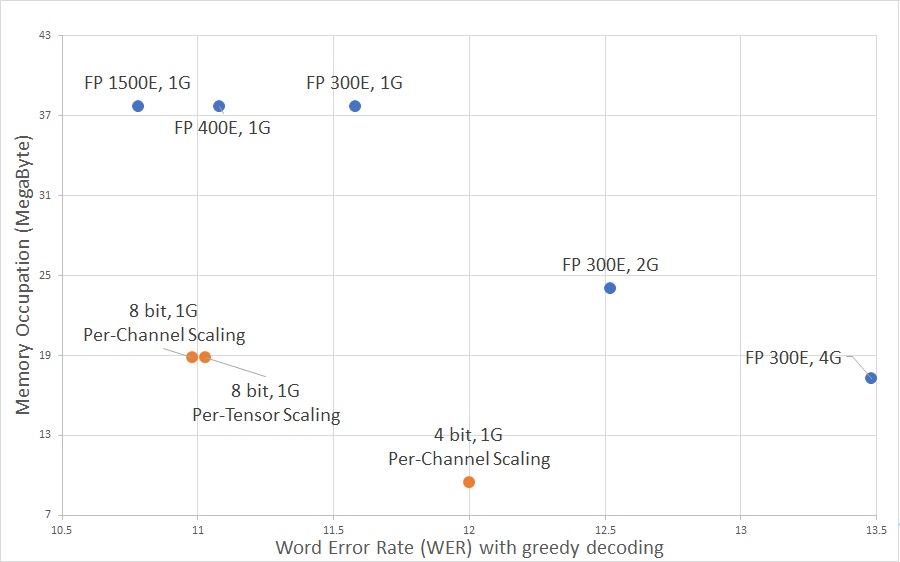Fig. 3 Memory footprint over WER on LibriSpeech dev-other

Fig. 4 Number of MACs Operations over WER on LibriSpeech dev-other

In evaluating the memory footprint, we consider half-precision (16 bit) Floating Point (FP) numbers for the original QuartzNet. As we can see on Fig. 3, the quantized implementations are able to achieve comparable accuracy compared to the corresponding floating-point verion, while greatly reducing the memory occupation. In the graph, the terms E stands for Epochs, while G for Groups, referring to the numbers of groups used for the grouped convolutions. In case of our 4 bit implementation, the first and last layer are left at 8 bit, but this is taken in account both in the computation of the memory occupation and of the number of operations. Notice how the 4 bit version is able to greatly reduce the memory footprint of the network compared to the grouped convolution variants, while still granting better accuracy.

For comparing accuracy against the number of multiply-accumulate (MAC), we consider 16 bit floating-point multiplications as 16 bit integer multiplications. This means that we are greatly underestimating the complexity of operations performed in the original floating-point QuartzNet model. Assuming a n^2 growth in the cost of integer multiplication, we consider a 4 bit MAC 16x less expensive than a 16 bit one. The number of MACs in the Fig. 2b is normalized with respect to 16 bit. Also in this case, it is clear to see that the quantized versions are able to greatly reduce the amount of operations required, with little-to-none degradation in accuracy. In particular, the 8 bit versions are already able to have a better WER and lower amount of MACs compared to the grouped convolutions, and this is confirmed also by the 4 bit version, with a little degradation in terms of WER.