2.1. Filters¶
The DSPLib contains several variants of Finite Impulse Response (FIR) filters. These include single-rate FIRs, half-band interpolation/decimation FIRs, as well as integer and fractional interpolation/decimation FIRs. More details in the Entry Point.
2.1.1. Entry Point¶
FIR filters have been categorized into classes and placed in a distinct namespace scope: xf::dsp::aie::fir, to prevent name collision in the global scope. Namespace aliasing can be utilized to shorten instantiations:
namespace dsplib = xf::dsp::aie;
Additionally, each FIR filter has been placed in its unique FIR type namespace. The available FIR filter classes and the corresponding graph entry point are listed below:
| Function | Namespace and class name |
|---|---|
| Single rate, asymmetrical | dsplib::fir::sr_asym::fir_sr_asym_graph |
| Single rate, symmetrical | dsplib::fir::sr_sym::fir_sr_sym_graph |
| Interpolation asymmetrical | dsplib::fir::interpolate_asym::fir_interpolate_asym_graph |
| Decimation, halfband | dsplib::fir::decimate_hb::fir_decimate_hb_graph |
| Interpolation, halfband | dsplib::fir::interpolate_hb::fir_interpolate_hb_graph |
| Decimation, asymmetric | dsplib::fir::decimate_asym::fir_decimate_asym_graph |
| Interpolation, fractional, asymmetric Note: superseded by resampler | dsplib::fir::interpolate_fract_asym:: fir_interpolate_fract_asym_graph |
| Interpolation or decimation, fractional, asymmetric | dsplib::fir::resampler::fir_resampler_graph |
| Decimation, symmetric | dsplib::fir::decimate_sym::fir_decimate_sym_graph |
2.1.2. Supported Types¶
All FIR filters can be configured for various types of data and coefficients. These types can be int16, int32, or float, and also real or complex. However, configurations with real data versus complex coefficients are not supported nor are configurations where the coefficents are a higher precision type than the data type. Data and coefficients must both be integer types or both be float types, as mixes are not supported.
The following table lists the supported combinations of data type and coefficient type.
| Data Type | |||||||
| Int16 | Cint16 | Int32 | Cint32 | Float | Cfloat | ||
| Coefficient type | Int16 | Supported | Supported | Supported | Supported | 3 | 3 |
| Cint16 | 1 | Supported | 1 | Supported | 3 | 3 | |
| Int32 | 2 | 2 | Supported | Supported | 3 | 3 | |
| Cint32 | 1, 2 | 2 | 1 | Supported | 3 | 3 | |
| Float | 3 | 3 | 3 | 3 | Supported | Supported | |
| Cfloat | 3 | 3 | 3 | 3 | 3 | Supported | |
|
|||||||
2.1.3. Template Parameters¶
The following table lists parameters common to all the FIR filters:
| Parameter Name | Type | Description | Range |
|---|---|---|---|
| TP_FIR_LEN | Unsigned int | The number of taps | Min - 4, Max - see Maximum FIR Length |
| TP_RND | Unsigned int | Round mode | 0 = truncate or floor 1 = ceiling 2 = positive infinity 3 = negative infinity 4 = symmetrical to infinity 5 = symmetrical to zero 6 = convergent to even 7 = convergent to odd |
| TP_SHIFT | Unsigned int | The number of bits to shift unscaled result down by before output. | 0 to 61 |
| TT_DATA | Typename | Data Type | int16, cint16, int32, cint32, float, cfloat |
| TT_COEFF | Typename | Coefficient type | int16, cint16, int32, cint32, float, cfloat |
| TP_INPUT_WINDOW_VSIZE | Unsigned int | The number of samples in the input window. For streams, it impacts the number of input samples operated on in a single iteration of the kernel. | Must be a multiple of the number of lanes used (typically 4 or 8). No enforced range, but large windows will result in mapper errors due to excessive RAM use, for windowed API implementations. |
| TP_CASC_LEN | Unsigned int | The number of cascaded kernels to use for this FIR. | 1 to 9. Defaults to 1 if not set. |
| TP_DUAL_IP | Unsigned int | Use dual inputs ports. An additional ‘in2’ input port will appear on the graph when set to 1. |
Range 0 (single input), 1 (dual input). Defaults to 0 if not set. |
| TP_USE_COEFF_RELOAD | Unsigned int | Enable reloadable coefficient feature. An additional ‘coeff’ RTP port will appear on the graph. |
0 (no reload), 1 (use reloads). Defaults to 0 if not set. |
| TP_NUM_OUTPUTS | Unsigned int | Number of fir output ports An additional ‘out2’ output port will appear on the graph when set to 2. |
1 to 2 Defaults to 1 if not set. |
| TP_API | Unsigned int | I/O interface port type | 0 = Window 1 = Stream |
| TP_SSR | Unsigned int | Parallelism factor | min=1 Defaults to 1 if not set. Max = limited by resource availability |
Note
The number of lanes is the number of data elements that are being processed in parallel. This varies depending on the data type (i.e., number of bits in each element) and the register or bus width.
For a list of template parameters for each FIR variant, see API Reference Overview.
TP_CASC_LEN describes the number of AIE processors to split the operation over, which allows resource to be traded for higher performance. TP_CASC_LEN must be in the range 1 (default) to 9. FIR graph instance consists of TP_CASC_LEN kernels and the FIR length (TP_FIR_LEN) is divided by the requested cascade length and each kernel in the graph gets assigned a fraction of the workload. Kernels are connected with cascade ports, which pass partial accumulation products downstream until last kernel in chain produces the output.
TP_DUAL_IP is an implementation trade-off between performance and resource utilization. Symmetric FIRs may be instanced with 2 input ports to alleviate the potential for memory read contention, which would otherwise result in stall cycles and therefore lower throughput. In addition, FIRs with streaming interface may utilize the second input port to maximize the available throughput.
When set to 0, the FIR is created with a single input port.
When set to 1, two input ports will be created.
Note
when used, port
port<input> in2;will be added to the FIR.
TP_USE_COEFF_RELOAD allows the user to select if runtime coefficient reloading should be used. When defining the parameter:
0 = static coefficients, defined in filter constructor
1 = reloadable coefficients, passed as argument to runtime function.
Note
when used, port
port<input> coeff;will be added to the FIR.
TP_NUM_OUTPUTS sets the number of output ports to send the output data to. Supported range: 1 to 2.
For Windows API, additional output provides flexibility in connecting FIR output with multiple destinations.
Additional output out2 is an exact copy of the data of the output port out.
Stream API uses the additional output port to increase the FIR’s throughput. Please refer to Stream Output for more details.
Note
when used, port port<output> out2; will be added to the FIR.
TP_SSR sets the parallelism factor. SSR is Super Sample Rate. It is supported for only the single rate asymmetic FIR at present. This setting allows for higher throughput at the expense of more tiles or kernels. The input data must be split over multiple ports where each successive sample is sent to a different input port in a round-robin fashion, i.e. sample 0 goes to input port in[0], sample 1 to in[1], etc up to N-1 where N=TP_SSR, then sample N goes to in[0], sample N+1 goes to in[1] and so on. Output samples are output from the multiple output ports in the same fashion. Where DUAL_IP is also enabled, there will be two sets of SSR input ports, in and in2. Allocate samples to ports 0 to N-1 of port in in the round robin fashion above until each port has 128bits of data, then allocate the next samples in a round robin fashion to ports 0 through N-1 of port in2 until these too have 128bits of data, then return to allocating samples to ports 0 through N-1 of in, and repeat.
If we have a data stream like int32 x = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, ..., then an SSR of 3 with dual ports would look something like this:
in[0] = 0, 3, 6, 9, 24, 27, 30, 33, ... in[1] = 1, 4, 7, 10, 25, 28, 31, 34, ... in[2] = 2, 5, 8, 11, 26, 29, 32, 35, ... in2[0] = 12, 15, 18, 21, 36, 39, 42, 45, ... in2[1] = 13, 16, 19, 22, 37, 40, 43, 46, ... in2[2] = 14, 17, 20, 23, 38, 41, 44, 47, ...
Note
TP_SSR is currently supported only for fir_sr_asym.
For more details, refer to Super Sample Rate Operation.
2.1.4. Access functions¶
For the access functions for each FIR variant, see API Reference Overview.
2.1.5. Ports¶
To see the ports for each FIR variants, see API Reference Overview. Note that some ports are present only for certain configurations of template parameters.
2.1.6. Design Notes¶
2.1.6.1. Coefficient array for Filters¶
2.1.6.1.1. Static coefficients¶
For all non-reloadable filter configurations, the coefficient values are passed as an array argument to the constructor (e.g.: std::array or std::vector).
2.1.6.1.2. Reloadable coefficients¶
Reloadable configurations do not require coefficient array passed through constructor at compile time. Instead, the graph’s update() (refer to UG1076 for usage instructions) method is used to pass coefficient array into kernels. update() method must be called after graph has been initialized, but before kernel starts operation on data samples.
2.1.6.1.3. Coefficients array size¶
Asymmetrical filters expect the full array of coefficients to be passed to kernel, i.e. coefficient array size is of the order of the filter. In the case of symmetrical filters, only the first half (plus any odd centre tap) need be passed, as the remaining may be derived by symmetry. For halfband filters, only the non-zero coefficients should be entered, with the centre tap last in the array. The length of the array expected will therefore be (TP_FIR_LEN+1)/4+1, e.g. for a halfband filter of length 11, 4 non-zero tap values, including the centre tap, are expected.
2.1.6.2. Window interface for Filters¶
On the AI Engine processor, data may be packetized into window buffers. In the case of FIRs, each window is extended by a margin so that the state of the filter at the end of the previous iteration of the window may be restored before new computations begin. Therefore, to maximize throughput, the window size should be set to the maximum that the system will allow, though this will lead to a corresponding increase in latency. For example, with a small window, say 32 samples, the overheads of window acquisition and release will be incurred for every 32 samples. Using a larger window will mean that a greater portion of time will be spent in active computation.
2.1.6.2.1. Maximum Window size¶
Window buffers are implemented using a ping-pong mechanism, where consumer kernel would read the ping portion of the buffer while producer would fill pong portion of the buffer that would be consumed in the next iteration. This approach maximizes performance, at the increased cost of memory storage. Window buffer is mapped into a single Memory Group in the area surrounding the kernel that accesses it. A Memory Group is 32 kB, and the maximum Window size should not exceed this limit.
2.1.6.2.2. Single buffer constraint¶
It is possible to disable the ping-pong mechanism, so that the entire available data memory is available to the kernel for computation. However, the single-buffered window can be accessed only by one agent at a time, and it comes with a performance penalty. This can be achieved by using the single_buffer() constraint that is applied to an input or output port of each kernel.
single_buffer(firGraph.getKernels()[0].in[0]);
2.1.6.3. Streaming interface for Filters¶
Streaming interfaces are now supported by all FIRs. When TP_API is set to 1 the FIR will have stream API input and output ports. Such filters have lower latency than window API filters because there is no window to fill before execution can begin.
2.1.6.3.1. Stream Output¶
Stream output allows computed data samples to be directly sent over the stream without the requirement for a ping-pong window buffer. As a result, memory use and latency are reduced. Furthermore, the streaming output allows data samples to be broadcast to multiple destinations.
To maximize the throughput, FIRs can be configured with 2 output stream ports. However, this may not improve performance if the throughput is bottlenecked by other factors, i.e., the input stream bandwidth or the vector processor. Set TP_NUM_OUTPUTS template parameter to 2, to create a FIR kernel with 2 output stream ports. In this scenario, the output data from the two streams is interleaved in chunks of 128 bits. E.g.:
- samples 0-3 to be sent over output stream 0 for cint16 data type,
- samples 4-7 to be sent over output stream 1 for cint16 data type.
2.1.6.3.2. Stream Input for Asymmetric FIRs¶
Stream input allows data samples to be directly written from the input stream to one of the Input Vector Registers without the requirement for a ping-pong window buffer. As a result, memory requirements and latency are reduced.
To maximize the throughput, FIRs can be configured with 2 input stream ports. Although this may not improve performance if the throughput is bottlenecked by other factors, i.e., the output stream bandwidth or the vector processor. Set TP_DUAL_IP to 1, to create a FIR instance with 2 input stream ports. In such a case the input data will be interleaved from the two ports to one data stream internally in 128 bit chunks, e.g.:
- samples 0-3 to be received on input stream 0 for cint16 data type,
- samples 4-7 to be received on input stream 1 for cint16 data type.
Note
For the single rate asymmetric option dual input streams offer no throughput gain if only single output stream would be used. Therefore, dual input streams are only supported with 2 output streams.
2.1.6.3.3. Stream Input for Symmetric FIRs¶
Symmetric FIRs require access to data from 2 distinctive areas of the data stream and therefore require memory storage. In symmetric FIRs the stream input is connected to an input ping-pong window buffer through a DMA port of a Memory Module.
2.1.6.4. Maximum FIR Length¶
The maximum FIR length which can be supported is limited by a variety of factors. Each of these factors, if exceeded, will result in a compile time failure with some indication of the nature of the limitation.
When using window-API for instance, the window buffer must fit into a 32kByte memory bank and since this includes the margin, it limits the maximum window size. Therefore, it also indirectly sets an upper limit on TP_FIR_LEN.
In addition, the single_buffer() constraint is needed to implement window buffers of > 16kB. Please refer to: Single buffer constraint for more details.
As a guide, a single rate symmetric FIR can support up to:
- 8k for 16-bit data, i.e. int16 data
- 4k for 32-bit data, i.e. cint16, int32, float
- 2k for 64-bit data, i.e. cint32, cfloat
Another limiting factor when considering implementation of high order FIRs is the Program Memory and sysmem requirements. Increasing FIR length requires greater amounts of heap and stack memory to store coefficients. Program Memory footpring also increses, as the number of instructions grows. As a result, a single FIR kernel can only support a limited amount of coefficents and longer FIRs have to be split up into a design consisting multiple FIR kernels using TP_CASC_LEN parameter.
When using stream based API, the architecture uses internal vector registers to store data samples, instead of window buffers, which removes the limiting factors of the window-based equivalent arhchitecture. However, the internal vector register is only 1024-bit wide, which greatly limits the amount of data samples each FIR kernel can operate on. In addition, data registers storage capacity will be affected by decimation factors, when a Decimation FIR is used. As a result, number of taps each AIE kernel can process, limited by the capacity of the input vector register, depends on a variety of factors, like data type, coefficient type and decimation factor.
To help find the number of FIR kernels required (or desired) to implement requested FIR length, please refer to helper functions: Minimum Cascade Length, Optimum Cascade Length described below.
2.1.6.5. Minimum Cascade Length¶
To help find the minimum supported TP_CASC_LEN value for a given configuration, the following utility functions have been created in file L1/include/aie/fir_common_traits.hpp, where the corresponding FIR variant is in the name of the function. In the following functions TP_API is 0 for window API and 1 for stream API. The return value is the minimum required TP_CASC_LEN for the FIR.
template<int TP_FIR_LEN, int TP_API, typename TT_DATA> constexpr int fnGetMinCascLenSrAsym(); template<int TP_FIR_LEN, int TP_API, typename TT_DATA> constexpr int fnGetMinCascLenSrSym(); template<int TP_FIR_LEN, int TP_API, typename TT_DATA> constexpr int fnGetMinCascLenIntHB(); template<int TP_FIR_LEN, int TP_API, typename TT_DATA> constexpr int fnGetMinCascLenDecHB(); template<int TP_FIR_LEN, int TP_API, typename TT_DATA, int T_INTERPOLATE_FACTOR> constexpr int fnGetMinCascLenIntAsym(); template<int TP_FIR_LEN, int TP_API, typename TT_DATA, typename TT_COEFF, int TP_DECIMATE_FACTOR> constexpr int fnGetMinCascLenDecAsym(); template<int TP_FIR_LEN, int TP_API, typename TT_DATA, int TP_DECIMATE_FACTOR> constexpr int fnGetMinCascLenDecSym();
An example of use within your graph constructor follows for the single rate asymmetric FIR variant, where all other parameters for the configuration you desire are called my* and kMinLen is the minimum supported TP_CASC_LEN value for myFirLen.
#include "fir_common_traits.hpp" ... static constexpr int kMinLen = xf::dsp::aie::fir::fnGetMinCascLenSrAsym<myFirLen, myPortApi, myDataType>(); xf::dsp::aie::fir::sr_asym::fir_sr_asym_graph<myDataType, myCoeffType, myFirLen, myShift, myRoundMode, myInputWindowSize, kMinLen, myCoeffReload, myNumOutputs, myDualIp, myPortApi, mySsr>;
2.1.6.6. Optimum Cascade Length¶
For FIR variants configured to use streaming interfaces, i.e. TP_API=1, the optimum TP_CASC_LEN for a given configuration of the other parameters is a complicated equation. Here, the optimum value of TP_CASC_LEN refers to the least number of kernels that the overall calculations can be divided, when the interface bandwidth limits the maximum performance. To aid in this determination, utility functions have been created for FIR variants in file fir_common_traits.hpp as follows, where the name of the FIR variant is in the name. In these functions, the parameter names are the same as for the configuration of the library element except for T_PORTS, where T_PORTS should be set to 1 for DUAL_IP=0 and NUM_OUTPUTS=1 or 2 when using DUAL_IP=1 and NUM_OUTPUTS=2.
template<int TP_FIR_LEN, typename TT_DATA, typename TT_COEFF, int TP_API, int T_PORTS> constexpr int fnGetOptCascLenSrAsym(); template<int TP_FIR_LEN, typename TT_DATA, typename TT_COEFF, int TP_API, int T_PORTS> constexpr int fnGetOptCascLenSrSym(); template<int TP_FIR_LEN, typename TT_DATA, typename TT_COEFF, int TP_API, int T_PORTS> constexpr int fnGetOptCascLenIntHB(); template<int TP_FIR_LEN, typename TT_DATA, typename TT_COEFF, int TP_API, int T_PORTS> constexpr int fnGetOptCascLenDecHB(); template<int TP_FIR_LEN, typename TT_DATA, typename TT_COEFF, int TP_API, int T_PORTS, int T_INTERPOLATE_FACTOR> constexpr int fnGetOptCascLenIntAsym(); template<int TP_FIR_LEN, typename TT_DATA, typename TT_COEFF, int TP_API, int T_PORTS, int T_DECIMATE_FACTOR> constexpr int fnGetOptCascLenDecAsym(); template<int TP_FIR_LEN, typename TT_DATA, typename TT_COEFF, int TP_API, int T_PORTS, int T_DECIMATE_FACTOR> constexpr int fnGetOptCascLenDecSym();
An example of use within your graph constructor follows from the single rate asymmetric FIR variant, where all other parameters for the configuration you desire are called my* and kOptLen is the optimum TP_CASC_LEN value.
#include "fir_common_traits.hpp" ... static constexpr int kOptLen = xf::dsp::aie::fir::fnGetOptCascLenSrAsym<myFirLen, myDataType, myCoeffType, myPortApi, myNumOutputs>(); xf::dsp::aie::fir::sr_asym::fir_sr_asym_graph<myDataType, myCoeffType, myFirLen, myShift, myRoundMode, myInputWindowSize, kOptLen, myCoeffReload, myNumOutputs, myDualIp, myPortApi, mySsr>;
2.1.6.7. Super Sample Rate Operation¶
While the term Super Sample Rate strictly means the processing of more than one sample per clock cycle, in the AIE context it is taken to mean an implementation using parallel kernels to improve performance at the expense of additional resource use. At present, only the Single Rate, Asymmetric FIR variant supports SSR operation. In the FIR, SSR operation is controlled by the template parameter TP_SSR.
The parameter TP_SSR allows a trade of performance for resource use in the form of tiles used. The number of tiles used by a FIR will be given by the formula
number of tiles = TP_CASC_LEN * TP_SSR * TP_SSR
Examples of this formula are given in Table 4.
| TP_SSR | TP_CASC_LEN | Number of tiles |
|---|---|---|
| 1 | 3 | 3 |
| 2 | 1 | 4 |
| 2 | 2 | 8 |
| 3 | 2 | 18 |
| 4 | 3 | 48 |
2.1.6.7.1. Super Sample Rate Sample to Port Mapping¶
When Super Sample Rate operation is used, data is input and output using multiple ports. These multiple ports on input or output act as one channel. The mapping of samples to ports is that each successive sample should be passed to a different port in a round-robin fashion, e.g. with TP_SSR set to 3, sample 0 should be sent to input port 0, sample 1 to input port 1, sample 2 to input port 2, sample 3 to input port 0 and so on. For more details, refer to TP_SSR.
2.1.6.8. Constraints¶
Should it be necessary to apply constraints within the FIR instance to achieve successful mapping of the design, you need to know the internal instance names for graph and kernel names. See Figure 1: Internal structure of FIR with TP_SSR=4 and TP_CASC_LEN=2 below.
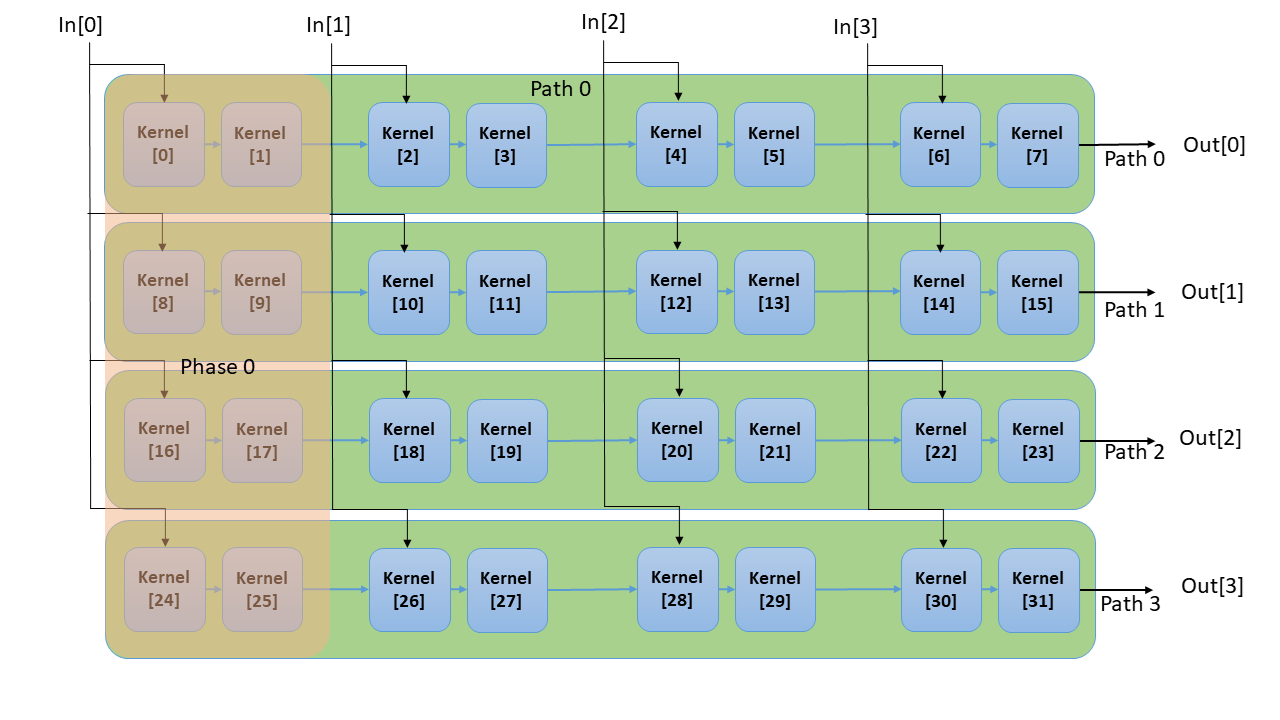
Figure 1: Internal structure of FIR with TP_SSR=4 and TP_CASC_LEN=2
Each FIR variant has a variety of access methods to help assign a constraint on a kernel and/or a net, e.g.:
- get_kernels() which returns a pointer to an array of kernel pointers, or
- getInNet() which returns a pointer to a net indexed by method’s argument(s).
More details are provided in the API Reference Overview.
An example of how to use this is given in the section Code Example including constraints. When configured for SSR operation, the FIR as a two-dimensional array (paths x phases) of units which are themselves FIRs, though each atomic FIR in this structure may itself be a series of kernels as described by TP_CASC_LEN. The access function get_kernels() returns a pointer to the array of kernels within the SSR FIR. This array will have TP_SSR * TP_SSR * TP_CASC_LEN members. The index in the array is determined by its path number, phase number and cascade position as shown in the following equation.
Kernel Index = Kernel Path * TP_SSR * TP_CASC_LEN + Kernel Phase * TP_CASC_LEN + Kernel Cascade index
For example, in a design with TP_CASC_LEN=2 and TP_SSR=3, the first kernel of the last path would have index 12.
The nets returned by the getInNet() function can be assigned custom fifo_depths values to override the defaults.
2.1.7. Code Example including constraints¶
The following code example shows how an FIR graph class may be used within a user super-graph, including example code to set the runtime ratio of kernels within the FIR graph class.
#include <adf.h> #include "fir_sr_sym_graph.hpp" #define LOC_XBASE 0 #define LOC_YBASE 0 #define DATA_TYPE cint16 #define COEFF_TYPE int16 #define TP_FIR_LEN 32 #define TP_SHIFT 0 #define TP_RND 0 #define TP_INPUT_WINDOW_VSIZE 256 #define TP_CASC_LEN 1 #define TP_USE_COEFF_RELOAD 0 #define TP_NUM_OUTPUTS 1 #define TP_API 0 class myFir : public adf::graph { public: adf::port<input> in; adf::port<output> out; std::vector<int16> taps = {1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}; xf::dsp::aie::fir::sr_sym::fir_sr_sym_graph<DATA_TYPE, COEFF_TYPE, TP_FIR_LEN, TP_SHIFT, TP_RND, TP_INPUT_WINDOW_VSIZE, TP_CASC_LEN, TP_USE_COEFF_RELOAD, TP_NUM_OUTPUTS, TP_API> filter; myFir() : filter(taps) { adf::kernel *filter_kernels = filter.getKernels(); adf::runtime<ratio>(*filter_kernels) = 0.515625; adf::location<kernel>(filter_kernels[0]) = tile(LOC_XBASE, LOC_YBASE); adf::connect<> net0(in , filter.in); adf::connect<> net1(filter.out , out); } };