Tridiagonal Matrix Solver

Overview

The Tridiagonal Matrix Solver solves a tridiagonal linear system using parallel cyclic reduction (also known as odd-even elimination). More details about this algorithm can be found in the paper: Penta Solver.

Implementation

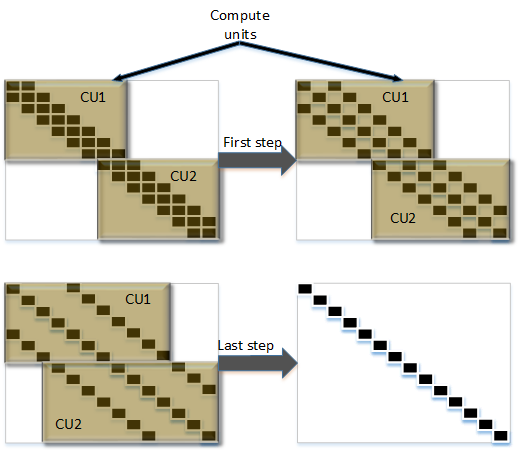
The solver works on a row-based scheme. For each row of diagonals it applies a reduction procedure. Each row is processed \(\log_2N -1\) times, which leads to a complete reduction of the upper and lower diagonals. The input matrix is stored as three vectors, one for each diagonal. Thanks to parallel nature of cyclic reduction algorithm, a parameterized number of compute units could be set to work simultaneously on one matrix; the whole matrix is then divided amongst a number of compute units.

Since the algorithm needs access to 3 consecutive rows of matrix only 3 rows are stored in at a time (for each compute unit). These allows algorithm to be fully pipelined and allow user to control performance and usage of resources.

Caution

Please note that the solver is very sensitive to zeros in main diagonal on input data. Due to the nature of the algorithm, any zeros on the main diagonal will lead to division-by-zero and the algorithm will fail.